《2025年新课程能力培养九年级数学上册人教版》

20. (8 分) 对于一元二次方程$ ax^{2}+bx + c = 0(a\neq0),$如果方程有两个实数根为$ x_{1},x_{2},$那么$ x_{1}+x_{2}= -\frac{b}{a},x_{1}\cdot x_{2}= \frac{c}{a}. $一元二次方程的这种根与系数的关系,最早是由法国数学家韦达 (1540-1603) 发现的,因此,我们把这个关系称为韦达定理,灵活运用这个定理有时可以使解题更为简单. 根据上述材料,结合你所学的知识,完成下列问题：
【材料理解】
已知一元二次方程$ x^{2}-3x - 2 = 0 $两个实数根分别为 m,n,求$ m^{2}n + mn^{2} $的值. 小明给出了一部分解题思路：
解：$\because $一元二次方程$ x^{2}-3x - 2 = 0 $的两个实数根分别为 m,n,
$\therefore m + n= ______,\therefore mn= ______,\therefore m^{2}n + mn^{2}=… .$
(1) 请将过程补充完整.
【类比应用】
(2) 一元二次方程$ -x^{2}+mx + 1 = 0 $的一个根为 x = 2,则 m= ______,另一个根为 x= ______.【思维拓展】(3) 关于 x 的一元二次方程$ x^{2}+(2m + 1)x + m^{2}-2 = 0 $有两个实数根,且这两个实数根的平方和是 21,求 m 的值.(1) 3，-2；$m^{2}n + mn^{2}=mn(m + n)=(-2)×3=-6(2) $$\frac{3}{2}$；$-\frac{1}{2}$(3) 方程$x^{2}+(2m + 1)x + m^{2}-2 = 0$中，a=1，b=2m+1，$c=m^2-2\Delta=(2m+1)^2-4×1×(m^2-2)=4m+9\geq0\Rightarrow m\geq-\frac{9}{4}$设两根为$x_1,x_2，$则$x_1+x_2=-(2m+1)，$$x_1x_2=m^2-2x_1^2+x_2^2=(x_1+x_2)^2-2x_1x_2=(2m+1)^2-2(m^2-2)=2m^2+4m+5=212m^2+4m-16=0\Rightarrow m^2+2m-8=0\Rightarrow(m+4)(m-2)=0\Rightarrow m=-4$或$m=2m=-4＜-\frac{9}{4}（$舍），$m=2\geq-\frac{9}{4}，$故m=2

答案：
(1) $3$，$-2$；$m^{2}n + mn^{2}=mn(m + n)=(-2)×3=-6$
(2) $\frac{3}{2}$；$-\frac{1}{2}$
(3) 方程$x^{2}+(2m + 1)x + m^{2}-2 = 0$中，$a=1$，$b=2m+1$，$c=m^2-2$
$\Delta=(2m+1)^2-4×1×(m^2-2)=4m+9\geq0\Rightarrow m\geq-\frac{9}{4}$
设两根为$x_1,x_2$，则$x_1+x_2=-(2m+1)$，$x_1x_2=m^2-2$
$x_1^2+x_2^2=(x_1+x_2)^2-2x_1x_2=(2m+1)^2-2(m^2-2)=2m^2+4m+5=21$
$2m^2+4m-16=0\Rightarrow m^2+2m-8=0\Rightarrow(m+4)(m-2)=0\Rightarrow m=-4$或$m=2$
$m=-4＜-\frac{9}{4}$（舍），$m=2\geq-\frac{9}{4}$，故$m=2$

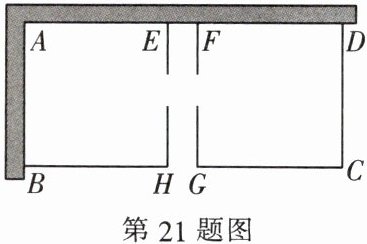
21. (8 分) 某农场要建一个饲养场(矩形 $ABCD$),两面靠墙($AD$ 位置的墙最大可用长度为 $27\mathrm{m}$,$AB$ 位置的墙最大可用长度为 $15\mathrm{m}$),另两边用木栏围成,中间也用木栏隔开,分成两个场地及一处通道,并在如图所示的三处各留 $1\mathrm{m}$ 宽的门(不用木栏). 建成后木栏总长 $45\mathrm{m}$.
(1) 若饲养场(矩形 $ABCD$)的一边 $CD$ 长为 $8\mathrm{m}$,则另一边 $BC= $24$\mathrm{m}$.
(2) 若饲养场(矩形 $ABCD$)的面积为 $180\mathrm{m^{2}}$,求边 $CD$ 的长.
(3) 饲养场的面积能达到 $210\mathrm{m^{2}}$ 吗？若能达到,求出边 $CD$ 的长；若不能达到,请说明理由.

(2) 设边 $ CD $ 的长为 $ y \, m $，边 $ BC $ 的长为 $ x \, m $。由题意得，木栏总长为水平方向3条木栏（$ CD $ 及两个分隔栏）减去3个门的长度加上竖直方向木栏 $ BC $ 的长度，即 $ x + 3y - 3 = 45 $，化简得 $ x = 48 - 3y $。
饲养场面积 $ S = x \cdot y = 180 $，代入 $ x = 48 - 3y $ 得：
$ (48 - 3y)y = 180 $
$ 3y^2 - 48y + 180 = 0 $
$ y^2 - 16y + 60 = 0 $
解得 $ y_1 = 10 $，$ y_2 = 6 $。
当 $ y = 6 $ 时，$ x = 48 - 3 × 6 = 30 \, m $，而 $ AD $ 墙最大可用长度为 $ 27 \, m $，$ 30 ＞ 27 $，舍去；当 $ y = 10 $ 时，$ x = 48 - 3 × 10 = 18 \, m \leq 27 \, m $，符合题意。
故边 $ CD $ 的长为 $ 10 \, m $。
(3) 假设面积能达到 $ 210 \, m^2 $，则 $ x \cdot y = 210 $，代入 $ x = 48 - 3y $ 得：
$ (48 - 3y)y = 210 $
$ 3y^2 - 48y + 210 = 0 $
$ y^2 - 16y + 70 = 0 $
判别式 $ \Delta = (-16)^2 - 4 × 1 × 70 = 256 - 280 = -24 ＜ 0 $，方程无实数根。
故饲养场面积不能达到 $ 210 \, m^2 $。

答案：
(1) 24
(2) 设边 $ CD $ 的长为 $ y \, m $，边 $ BC $ 的长为 $ x \, m $。由题意得，木栏总长为水平方向3条木栏（$ CD $ 及两个分隔栏）减去3个门的长度加上竖直方向木栏 $ BC $ 的长度，即 $ x + 3y - 3 = 45 $，化简得 $ x = 48 - 3y $。
饲养场面积 $ S = x \cdot y = 180 $，代入 $ x = 48 - 3y $ 得：
$ (48 - 3y)y = 180 $
$ 3y^2 - 48y + 180 = 0 $
$ y^2 - 16y + 60 = 0 $
解得 $ y_1 = 10 $，$ y_2 = 6 $。
当 $ y = 6 $ 时，$ x = 48 - 3 × 6 = 30 \, m $，而 $ AD $ 墙最大可用长度为 $ 27 \, m $，$ 30 ＞ 27 $，舍去；当 $ y = 10 $ 时，$ x = 48 - 3 × 10 = 18 \, m \leq 27 \, m $，符合题意。
故边 $ CD $ 的长为 $ 10 \, m $。
(3) 假设面积能达到 $ 210 \, m^2 $，则 $ x \cdot y = 210 $，代入 $ x = 48 - 3y $ 得：
$ (48 - 3y)y = 210 $
$ 3y^2 - 48y + 210 = 0 $
$ y^2 - 16y + 70 = 0 $
判别式 $ \Delta = (-16)^2 - 4 × 1 × 70 = 256 - 280 = -24 ＜ 0 $，方程无实数根。
故饲养场面积不能达到 $ 210 \, m^2 $。