8. 如图,为了估算河的宽度,小明采用的办法是:在河的对岸选取一点$A$,在近岸取点$D$,$B$,使得$A$,$D$,$B$在一条直线上,且与河的边沿$DE$垂直,然后又在垂直于$AB的直线上取点C$,并测得$BD = 15m$,$BC = 40m$. 如果$DE = 30m$,则河宽$AD$为(

A.$30m$
B.$35m$
C.$40m$
D.$45m$
D
)
A.$30m$
B.$35m$
C.$40m$
D.$45m$
答案:
D
9. 如图,线段$AB的两个端点坐标分别为A(4,6)$,$B(6,3)$,以原点$O$为位似中心,将线段$AB在第一象限缩小为原来的\frac{1}{2}$,则点$A的对应点C$的坐标为(
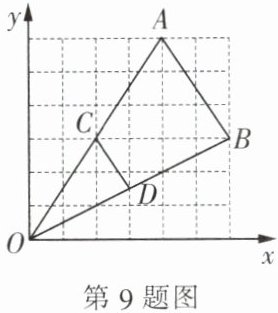
A.$(2,3)$
B.$(3,2)$
C.$(3,\frac{3}{2})$
D.$(\frac{3}{2},3)$
A
)
A.$(2,3)$
B.$(3,2)$
C.$(3,\frac{3}{2})$
D.$(\frac{3}{2},3)$
答案:
A
10. 如图,$\triangle ABC内接于\odot O$,点$D在\odot O$上,连接$CD交AB于点E$,若$AC = BC = 2$,$CE = 1$,则$CD$的长为(

A.8
B.6
C.5
D.4
D
)
A.8
B.6
C.5
D.4
答案:
D
11. 如图,四边形$ABCD\sim四边形A'B'C'D'$,则$\angle D'$的度数为
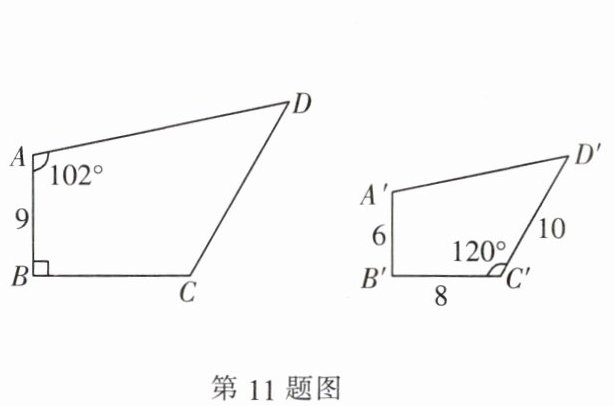
108°
.
答案:
108°
12. 如图 1,“矩”在古代指两条边成直角的曲尺,它的两边长分别为$a$,$b$. 中国古老的天文和数学著作《周髀算经》中简明扼要地阐述了“矩”的功能,如“偃矩以望高”的意思就是把“矩”仰立放可测物体的高度. 如图 2,从“矩”$AFE的一端A望向树顶端的点C$,使视线通过“矩”的另一端$E$,测得$AB = 1.5m$,$BD = 6.2m$. 若“矩”的边$EF = a = 30cm$,边$AF = b = 60cm$,则树高$CD$为

4.6
$m$.
答案:
4.6
13. 如图是凸透镜成像示意图,$CD是蜡烛AB通过凸透镜MN$所成的虚像,已知蜡烛的高$AB为4.8cm$,蜡烛$AB离凸透镜MN的水平距离OB为6cm$,该凸透镜的焦距$OF为10cm$,$AE// OF$,则像$CD$的高为
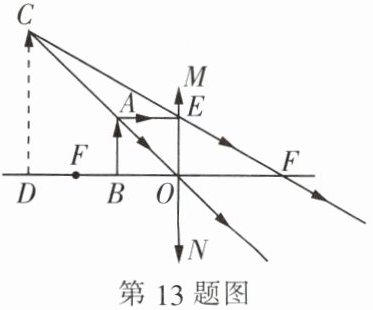
12
$cm$.
答案:
12
查看更多完整答案,请扫码查看


