《2025年新课程能力培养九年级数学上册人教版》

13. 已知反比例函数 $ y = \frac{k}{x} $ 的图象在第二、第四象限内, 函数图象上有两点 $ A(2, y_1) $, $ B(5, y_2) $, 则 $ y_1 $ 与 $ y_2 $ 的大小关系为$y_1 ＜ y_2$.

答案： $y_1 ＜ y_2$

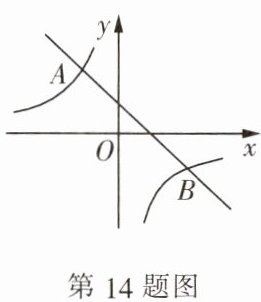
14. 如图, 一次函数 $ y = kx + b $ 的图象与反比例函数 $ y = -\frac{2}{x} $ 的图象相交于 $ A(-1, m) $ 和 $ B(n, -1) $ 两点, 结合图象直接写出不等式 $ kx + b ＞ -\frac{2}{x} $ 的解集$x\lt - 1$或$0\lt x\lt 2$.

答案： $x\lt - 1$或$0\lt x\lt 2$

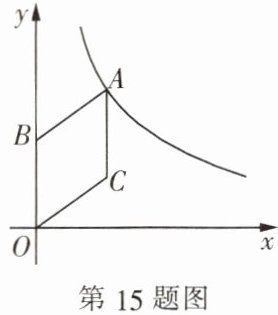
15. 如图, 在平面直角坐标系中, 菱形 $ ABOC $ 的顶点 $ A $ 在反比例函数 $ y = \frac{k}{x} $ ($ k ＞ 0 $, $ x ＞ 0 $) 的图象上, 点 $ C $ 的坐标为 $ (4, 3) $, 则 $ k $ 的值为32.

答案： 32

16. (10 分) 已知 $ y $ 与 $ x $ 成反比例, 且当 $ x = -3 $ 时, $ y = 7 $.
(1) 写出 $ y $ 与 $ x $ 之间的函数表达式.
(2) 当 $ x = -3 $ 时, 求 $ y $ 的值.
(3) 若 $ y $ 的取值范围是 $ -3 \leq y \leq 3 $, 求 $ x $ 的取值范围.

答案：
(1) 设 $y = \frac{k}{x}$（其中 $k \neq 0$）。
将 $x = -3$，$y = 7$ 代入得：
$7 = \frac{k}{-3} \implies k = -21$，
因此，$y$ 与 $x$ 之间的函数表达式为：
$y = -\frac{21}{x}$。
(2) 当 $x = -3$ 时，代入 $y = -\frac{21}{x}$ 得：
$y = -\frac{21}{-3} = 7$。
(3) 当 $-3 \leq y \leq 3$ 时，
对于 $y = -3$，代入 $y = -\frac{21}{x}$ 得：
$-3 = -\frac{21}{x} \implies x = 7$，
对于 $y = 3$，代入 $y = -\frac{21}{x}$ 得：
$3 = -\frac{21}{x} \implies x = -7$，
由于 $y$ 与 $x$ 成反比例，且 $k ＜ 0$，
当 $y$ 从 $-3$ 增加到 $3$，$x$ 从 $7$ 减小到 $-7$，
因此，$x$ 的取值范围为：
$x \leq -7$ 或 $x \geq 7$。