14. 如图,正方形网格图中的$\triangle ABC与\triangle A'B'C'$是位似关系图,则位似中心是点$R$、点$P$、点$Q$、点$O$四个点中的

P
.
答案:
【解析】:连接对应点A与A'、B与B'、C与C',三条直线相交于点P,故位似中心是点P。
【答案】:P
【答案】:P
15. 如图,平行四边形$ABCD的对角线AC$,$BD相交于点O$,过点$B作BE// AC$,交$DA的延长线于点E$,连接$OE$,交$AB于点F$,则四边形$BCOF的面积与\triangle AEF$的面积的比值为______

5/2
.
答案:
5/2
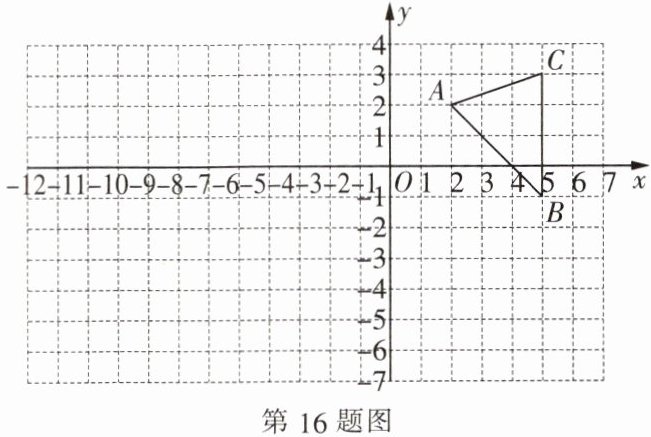
16. (10 分) 如图,在平面直角坐标系中,$\triangle ABC的三个顶点的坐标分别为A(2,2)$,$B(5,-1)$,$C(5,3)$.
(1) 点$B$关于原点对称的点的坐标为______.
(2) 请以原点$O$为位似中心,在$y轴左侧画一个\triangle A_{1}B_{1}C_{1}$,使$\triangle A_{1}B_{1}C_{1}与\triangle ABC$位似,且相似比为$2:1$,点$A$,$B$,$C的对应点分别为A_{1}$,$B_{1}$,$C_{1}$.
(1) 点$B$关于原点对称的点的坐标为______.
(2) 请以原点$O$为位似中心,在$y轴左侧画一个\triangle A_{1}B_{1}C_{1}$,使$\triangle A_{1}B_{1}C_{1}与\triangle ABC$位似,且相似比为$2:1$,点$A$,$B$,$C的对应点分别为A_{1}$,$B_{1}$,$C_{1}$.

答案:
(1) (-5,1)
(2) 解:
∵ 以原点O为位似中心,相似比为2:1,且在y轴左侧,
∴ 点A₁、B₁、C₁的坐标分别为:
A₁(2×(-2), 2×(-2)) = (-4, -4),
B₁(5×(-2), -1×(-2)) = (-10, 2),
C₁(5×(-2), 3×(-2)) = (-10, -6)。
连接A₁B₁、B₁C₁、C₁A₁,得△A₁B₁C₁。

(1) (-5,1)
(2) 解:
∵ 以原点O为位似中心,相似比为2:1,且在y轴左侧,
∴ 点A₁、B₁、C₁的坐标分别为:
A₁(2×(-2), 2×(-2)) = (-4, -4),
B₁(5×(-2), -1×(-2)) = (-10, 2),
C₁(5×(-2), 3×(-2)) = (-10, -6)。
连接A₁B₁、B₁C₁、C₁A₁,得△A₁B₁C₁。
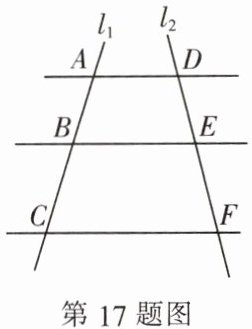
17. (8 分) 如图,已知$AD// BE// CF$,它们依次交直线$l_{1}$,$l_{2}于点A$,$B$,$C和点D$,$E$,$F$,且$AB = 6$,$BC = 8$,$DE = 3$,求$DF$的长.

答案:
∵AD//BE//CF,
∴$\frac{AB}{BC}=\frac{DE}{EF}$。
∵AB=6,BC=8,DE=3,
∴$\frac{6}{8}=\frac{3}{EF}$,
解得EF=4。
∴DF=DE+EF=3+4=7。
答:DF的长为7。
∵AD//BE//CF,
∴$\frac{AB}{BC}=\frac{DE}{EF}$。
∵AB=6,BC=8,DE=3,
∴$\frac{6}{8}=\frac{3}{EF}$,
解得EF=4。
∴DF=DE+EF=3+4=7。
答:DF的长为7。
查看更多完整答案,请扫码查看


