第76页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
12. 如图,有$5$张写着不同数的卡片,请你按要求借助卡片上的数完成下列各题:
$\boxed{-3}$ $\boxed{-2}$ $\boxed{-6.5}$ $\boxed{+3}$ $\boxed{+4}$
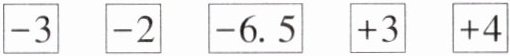
(1)从中取出$2$张卡片,使卡片上的$2$个数的和最小,则取出的数是______和______,和的最小值是______;
(2)从中取出$2$张卡片,使卡片上的$2$个数的差最大,则取出的数是______和______,差的最大值是______;
(3)从中取出$2$张卡片,使卡片上的$2$个数的积最小,则取出的数是______和______,积的最小值是______;
(4)从中取出$2$张卡片,使卡片上的$2$个数的商最大,则取出的数是______和______,商的最大值是______;
(5)再制作$1$张写有数的卡片,使$6张卡片上的数之和为0$,则新制作的卡片上的数应写多少?
$\boxed{-3}$ $\boxed{-2}$ $\boxed{-6.5}$ $\boxed{+3}$ $\boxed{+4}$
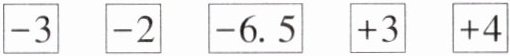
(1)从中取出$2$张卡片,使卡片上的$2$个数的和最小,则取出的数是______和______,和的最小值是______;
(2)从中取出$2$张卡片,使卡片上的$2$个数的差最大,则取出的数是______和______,差的最大值是______;
(3)从中取出$2$张卡片,使卡片上的$2$个数的积最小,则取出的数是______和______,积的最小值是______;
(4)从中取出$2$张卡片,使卡片上的$2$个数的商最大,则取出的数是______和______,商的最大值是______;
(5)再制作$1$张写有数的卡片,使$6张卡片上的数之和为0$,则新制作的卡片上的数应写多少?
答案:
(1)-3 -6.5 -9.5
(2)+4 -6.5 10.5
(3)-6.5 +4 -26
(4)-2 -6.5 3.25
(5)新制作的卡片上的数应写4.5.
(1)-3 -6.5 -9.5
(2)+4 -6.5 10.5
(3)-6.5 +4 -26
(4)-2 -6.5 3.25
(5)新制作的卡片上的数应写4.5.
13. 阅读下列内容,并完成相关问题。
小明学习了有理数的运算后,定义了一种新的运算,叫$*$(加乘)运算,然后他写出了一些按照$*$(加乘)运算的运算法则进行运算的算式:$( + 4 ) * ( + 2 ) = + 6$;$( - 4 ) * ( - 3 ) = + 7$;$( + 5 ) * ( - 3 ) = - 8$;$( + 6 ) * ( - 4 ) = - 10$;$( + 8 ) * 0 = 8$;$0 * ( - 9 ) = 9$。
小亮看了这些算式后说:“我知道你定义的$*$(加乘)运算的运算法则了。”
聪明的你也明白了吗?请你帮忙归纳$*$(加乘)运算的运算法则:
(1)归纳$*$(加乘)运算的运算法则:
两数进行$*$(加乘)运算时,同号得______,异号得______,并把两数的绝对值______。特别地,$0和任何数进行*$(加乘)运算或任何数和$0进行*$(加乘)运算时,都等于这个数的______。
(2)模仿计算:
$( - 4 ) * ( + 3 ) = $______;
$( + 3 ) * ( - 4 ) = $______;
$( - 5 ) * ( - 7 ) = $______;
$0 * ( - \pi ) = $______。
(3)拓展计算:
$[ ( - 2 ) * ( + 3 ) ] * [ ( - 12 ) * 0 ]$。(括号的作用与它在有理数运算中的作用一致)
(4)深入思考:
我们知道加法有交换律和结合律,这两种运算律在有理数的$*$(加乘)运算中还适用吗?请你任选一个运算律,判断它在$*$(加乘)运算中是否适用,并举一个例子验证。
小明学习了有理数的运算后,定义了一种新的运算,叫$*$(加乘)运算,然后他写出了一些按照$*$(加乘)运算的运算法则进行运算的算式:$( + 4 ) * ( + 2 ) = + 6$;$( - 4 ) * ( - 3 ) = + 7$;$( + 5 ) * ( - 3 ) = - 8$;$( + 6 ) * ( - 4 ) = - 10$;$( + 8 ) * 0 = 8$;$0 * ( - 9 ) = 9$。
小亮看了这些算式后说:“我知道你定义的$*$(加乘)运算的运算法则了。”
聪明的你也明白了吗?请你帮忙归纳$*$(加乘)运算的运算法则:
(1)归纳$*$(加乘)运算的运算法则:
两数进行$*$(加乘)运算时,同号得______,异号得______,并把两数的绝对值______。特别地,$0和任何数进行*$(加乘)运算或任何数和$0进行*$(加乘)运算时,都等于这个数的______。
(2)模仿计算:
$( - 4 ) * ( + 3 ) = $______;
$( + 3 ) * ( - 4 ) = $______;
$( - 5 ) * ( - 7 ) = $______;
$0 * ( - \pi ) = $______。
(3)拓展计算:
$[ ( - 2 ) * ( + 3 ) ] * [ ( - 12 ) * 0 ]$。(括号的作用与它在有理数运算中的作用一致)
(4)深入思考:
我们知道加法有交换律和结合律,这两种运算律在有理数的$*$(加乘)运算中还适用吗?请你任选一个运算律,判断它在$*$(加乘)运算中是否适用,并举一个例子验证。
答案:
(1)正 负 相加 绝对值
(2)-7 -7 12 π
(3)$[(-2)*(+3)]*[(-12)*0]$
$=(-5)*12$
$=-17.$
(4)加乘运算的交换律仍然适用.
如:$(-3)*(-5)=8,(-5)*(-3)=8$,所以$(-3)*(-5)=(-5)*(-3).$
加乘运算的结合律不适用.
如:$[(-3)*(-5)]*0=8*0=8,(-3)*[(-5)*(0)]=(-3)*5=-8,$
所以$[(-3)*(-5)]*0≠(-3)*[(-5)*$
(0)],结合律不适用.
(1)正 负 相加 绝对值
(2)-7 -7 12 π
(3)$[(-2)*(+3)]*[(-12)*0]$
$=(-5)*12$
$=-17.$
(4)加乘运算的交换律仍然适用.
如:$(-3)*(-5)=8,(-5)*(-3)=8$,所以$(-3)*(-5)=(-5)*(-3).$
加乘运算的结合律不适用.
如:$[(-3)*(-5)]*0=8*0=8,(-3)*[(-5)*(0)]=(-3)*5=-8,$
所以$[(-3)*(-5)]*0≠(-3)*[(-5)*$
(0)],结合律不适用.
查看更多完整答案,请扫码查看


