《2025年名校课堂七年级数学上册华师大版》

2. 【综合实践】我们在“图形的初步认识”这一章“数学活动”中探究了“如何制作包装盒”，小明和小亮在课后对“如何制作正方体纸盒”又进行了探究：


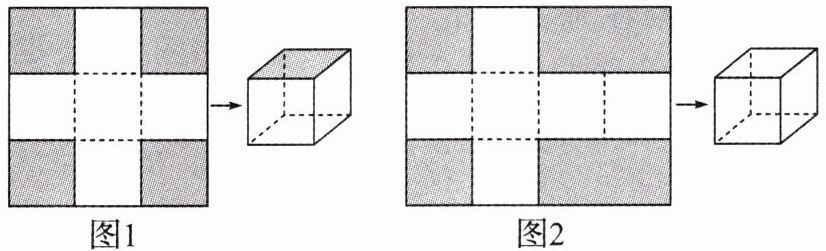
【动手操作】小明用一张正方形纸板按如图1所示的方式先在纸板四角剪去四个同样大小的小正方形，再沿虚线折合起来就可以做成一个无盖的正方体纸盒.
小亮用一张长方形纸板按如图2所示的方式先在纸板四角剪去两个同样大小的小正方形和两个同样大小的小长方形，将剩余部分折合起来可以制作一个有盖的正方体纸盒(纸板厚度及接缝处忽略不计).
【问题解决】现有一块长为$a$cm、宽为$b$cm的长方形纸板，请探究：
(1) 若$a = b$，按图1的方式剪去的小正方形边长为$c$cm，做成一个无盖的正方体纸盒，此时$c$与$b$之间存在的数量关系为；
(2) 若$a＞b$，按图2的方式裁剪，做成一个有盖的正方体纸盒，则$a$与$b$之间存在的数量关系是；
(3) 在(2)的条件下，若$a = 8$，求有盖正方体纸盒的表面积.

答案：
(1) $ b = 3c $
(2) $ a = 2b $
(3) 由
(2)知 $ a = 2b $，$ a = 8 $，则 $ b = 4 $。设正方体棱长为 $ x $，则 $ b = 2x $，$ x = 2 $。表面积 $ 6x^2 = 6×2^2 = 24 \, cm^2 $。
24