《2025年名校课堂七年级数学上册华师大版》

1. 下列关于数轴的说法不正确的是()

A.数轴上的单位长度必须相等
B.规定直线上从原点向左的方向为正方向
C.数轴上的原点可以任意选取
D.数轴是规定了原点、正方向、单位长度的一条直线

答案： B

2. 四位同学画的数轴如图所示，其中正确的是()

答案： D

3. 如图，点$A$表示；点$B$表示；点$C$表示；点$D$表示.
]

答案： 1；-1；2.5；-1.5

4. (教材$P9$练习$T2$变式)填空：
(1)数轴上在原点右边，且距离原点$3.7$个单位长度的点表示的数是；
(2)数轴上在原点左边，且距离原点$\dfrac{5}{8}$个单位长度的点表示的数是.

答案：
(1) $3.7$
(2) $-\dfrac{5}{8}$

5. ($2024$·苏州)用数轴上的点表示下列各数，其中与原点距离最近的是()

A.$-3$
B.$1$
C.$2$
D.$3$

答案： B

6. ($2023$·开封月考)如图，数轴的单位长度为$1$.如果点$A$表示的数是$-1$，那么点$B$表示的数是()


A.$0$
B.$1$
C.$2$
D.$3$

答案： D

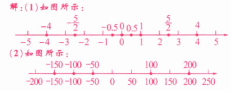
7. （教材$P12$习题$T2$变式）在数轴上表示下列各数：
（1）$0.5$，$-\dfrac{5}{2}$，$0$，$-4$，$\dfrac{5}{2}$，$-0.5$，$1$，$4$；
（2）$200$，$-150$，$-50$，$100$，$-100$.

答案：

8. (1)在数轴上距离原点$6$个单位长度的点所表示的数是；
(2)($2024$·郑州七中月考)数轴上与表示$-2$的点的距离为$6$个单位长度的点所表示的数是.

答案：
(1) $\pm 6$；
(2) $-8$或$4$（或 $4$或$-8$）

9. （$2024$·南阳月考）在数轴上，已知点$A$所表示的数为$-2$，则点$A$沿数轴移动$4$个单位长度后所表示的数是.

答案： $2$或$-6$（根据题目要求，若为填空题需明确两个结果，若为选择题则根据选项选择，此处按自由输入处理，填具体值）
由于题目要求填空，答案为：
2或-6
若为选择题，根据选项标记（但题目未给选项），此处按文本要求直接填数值。

10. 在一条不完整的数轴上从左到右有$A$，$B$，$C$三点，其中$A$，$B$两点的距离是$2$个单位长度，$B$，$C$两点的距离是$1$个单位长度，如图所示.

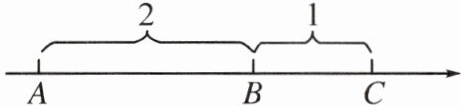
（1）若以$B$为原点，写出点$A$，$C$所表示的数；若以$C$为原点，写出点$A$，$B$所表示的数；
（2）若原点$O$在点$C$的右边，且$C$，$O$两点的距离为$8$个单位长度，写出点$A$，$B$，$C$所表示的数.

答案： （1）以B为原点：A=-2，C=1；以C为原点：A=-3，B=-1；
（2）A=-11，B=-9，C=-8。

11. 综合与实践
【问题情境】
邮递员从邮局出发，先向西骑行$3km$到达$A$村，继续向西骑行$2km$到达$B$村，然后向东骑行$9km$到达$C$村，最后回到邮局.
【提出问题】
（1）如图，请在以邮局为原点，向东为正方向，$1km$为$1$个单位长度的数轴上表示出$A$，$B$，$C$三个村庄的位置；
【问题拓展】
（2）$C$村离$A$村有多远？
（3）求邮递员一共骑行的路程.
]

答案：
（1）A村：-3，B村：-5，C村：4。（在数轴上对应位置标出即可）

（2）4 - (-3) = 7(km)
（3）3 + 2 + 9 + 4 = 18(km)