《2025年名校课堂七年级数学上册华师大版》

1. 用代数式表示：$x$与$y$的$2$倍的和. 下列表示正确的是()

A.$2x + y$
B.$x + 2y$
C.$2(x + y)$
D.$2xy$

答案： B

2. 用代数式表示：
(1)$x$与它的$\frac{1}{2}$的差：；
(2)$a$与$b$的和的$3$倍：；
(3)$x$与$2$的和的倒数：；
(4)$a$，$b$两数的立方和：；
(5)$a$，$c$两数差的立方：.

答案：
(1) $x - \frac{1}{2}x$；
(2) $3(a + b)$；
(3) $\frac{1}{x + 2}$；
(4) $a^3 + b^3$；
(5) $(a - c)^3$

3. 若$n$表示任意一个整数，则奇数可表示为，偶数可表示为.

答案： 2n+1（或2n-1）；2n

4. 按一定规律排列的数字：$\frac{1}{3}$，$\frac{1}{5}$，$\frac{1}{7}$，$\frac{1}{9}$，…，第$n$个数用代数式表示为.

答案： $\frac{1}{2n+1}$

5. (2024·洛阳西工区期中)代数式$-7x$的意义可以是()

A.$-7$与$x$的和
B.$-7$与$x$的差
C.$-7$与$x$的积
D.$-7$与$x$的商

答案： C

6. 写出下列各代数式的意义：
(1)$2(a + 3)$；(2)$x^{2}+y^{2}$；(3)$\frac{n + 1}{n - 1}$.

答案：
(1)a与3的和的2倍；
(2)x的平方与y的平方的和；
(3)n与1的和除以n与1的差的商.

7. (教材 P89 习题 T6 变式)设$m$为整数，则“被$3$除余$1$的整数”可以用整数$m$表示为()

A.$3m - 1$
B.$\frac{m}{3}-1$
C.$\frac{m}{3}+1$
D.$3m + 1$

答案： D

8. 1905 年清朝学堂的课本中用“$\frac{五}{甲^{二}}-\frac{三}{丙}+\frac{四}{甲乙^{二}}$”来表示代数式$\frac{a^{2}}{5}-\frac{c}{3}+\frac{ab^{2}}{4}$，则“$\frac{三}{甲^{二}乙^{二}}+\frac{二}{甲^{二}乙^{二}}$”表示的代数式为()

A.$\frac{ab^{2}}{3}+\frac{a^{2}b}{2}$
B.$\frac{ab^{2}}{3}-\frac{a^{2}b}{2}$
C.$\frac{3}{ab^{2}}+\frac{2}{a^{2}b}$
D.$\frac{3}{ab^{2}}-\frac{2}{a^{2}b}$

答案： 【解析】：根据题意，清朝课本中“汉字数字/代数式部分”对应现代代数式“代数式部分/数字”，其中“甲”对应“a”，“乙”对应“b”，“丙”对应“c”，汉字数字对应阿拉伯数字。
“三/甲乙²”对应“ab²/3”（“三”对应3，“甲乙²”对应ab²）；
“二/甲²乙”对应“a²b/2”（“二”对应2，“甲²乙”对应a²b）。
故“三/甲乙² + 二/甲²乙”表示“ab²/3 + a²b/2”。
【答案】：A

9. (2024·南阳邓州市期中)代数式$a^{2}-\frac{1}{b}$的正确解释是()

A.$a$与$b$的倒数的差的平方
B.$a$的平方与$b$的倒数的差
C.$a$的平方与$b$的差的倒数
D.$a$与$b$的差的平方的倒数

答案： B

10.
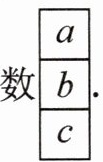
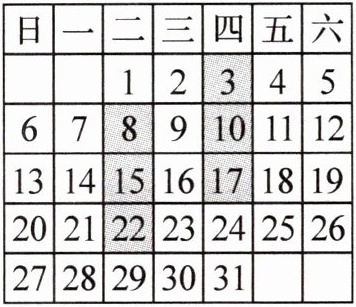
如图，用长方形任意框出某月历表上的$3$个数$\begin{array}{|c|}\hline a\\\hline b\\\hline c\\\hline\end{array}$. 若$a = k$，则$b$，$c$分别可表示为，（用含$k$的代数式表示）.

答案： $k + 7$，$k + 14$

11. (2024·南阳方城县期中)已知数轴上的点$A$，$B$所表示的数分别为$m$，$n$，则到点$A$，$B$的距离相等的点所表示的数为____.（用含$m$，$n$的代数式表示）

答案： $\frac{m + n}{2}$

12. 用代数式表示：
(1)三个连续的整数（用同一个字母表示）；
(2)$a$与$b$的差与$c$的平方的和；
(3)百位数字是$a$、十位数字是$b$、个位数字是$c$的三位数.

答案：
(1)设中间的整数为$n$，则三个连续整数为$n - 1$，$n$，$n + 1$。
(2)$(a - b) + c^2$
(3)$100a + 10b + c$