《2025年名校课堂七年级数学上册华师大版》

10. 如图，这是我国某一古建筑的主视图，最符合视图特点的建筑物的是()

答案： C

11. (2023·呼和浩特)如图，这是某几何体的三视图，则这个几何体是()

答案： C

12. (2024·宁夏)用 5 个大小相同的小正方体搭一个几何体，其主视图、左视图如图 2 所示.现将其中 4 个小正方体按如图 1 所示的方式摆放，则最后一个小正方体应放在()


A.①号位置
B.②号位置
C.③号位置
D.④号位置

答案： B

13. 如果一个几何体是由多个小正方体堆成，其三视图如图所示，那么这样的几何体一共有个小正方体.

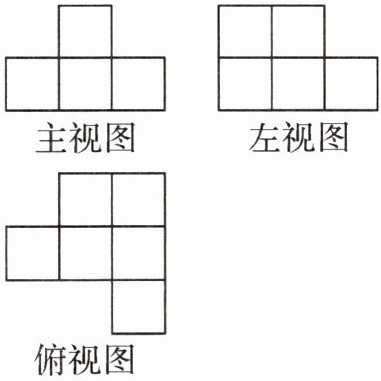
答案： 8

14. 如图所示的是一个几何体的三视图.
(1)这个几何体的名称是；
(2)由图中尺寸，计算这个几何体的表面积.

答案：
(1)
圆柱
(2)
主视图和俯视图可知几何体为圆柱，底面直径为$6$，高为$10$，
底面半径$r = \frac{6}{2}=3$，
底面积$S_{底}=\pi r^{2}=\pi×3^{2} = 9\pi$，
两底面积$2S_{底}=2×9\pi = 18\pi$，
侧面积$S_{侧}=2\pi r× h=2\pi×3×10 = 60\pi$，
表面积$S = 2S_{底}+S_{侧}=18\pi + 60\pi=78\pi$。

15. (2024·南阳方树泉中学月考)学校食堂厨房的桌子上整齐地叠放着若干个相同规格的碟子，碟子的个数与碟子高度的关系如下表：

(1)当桌子上叠放了 $ x $ 个碟子时，请写出此时碟子的高度(用含 $ x $ 的代数式表示)；
(2)桌子上摆放着一些碟子，它们的三视图如图所示，厨房师傅想把它们整齐叠成一摞，求叠成一摞后的高度.

答案：
(1) 由表格可知，1个碟子高度为2cm，每增加1个碟子高度增加1.5cm。当有x个碟子时，高度为$2 + 1.5(x - 1)$，化简得$1.5x + 0.5$。故答案为$(1.5x + 0.5)\ cm$。
(2) 由俯视图知有3摞碟子，结合主视图和左视图可得各摞碟子数分别为4、2、3，总个数$x = 4 + 2 + 3 = 9$。将$x = 9$代入$1.5x + 0.5$，得$1.5×9 + 0.5 = 14$。故叠成一摞后的高度为$14\ cm$。
(1)$1.5x + 0.5$
(2)$14\ cm$