第58页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
【例】已知 $a,b,c$ 在数轴上的对应点的位置如图所示,且 $|a|=|c|$。
(1)填空:$a + b$$0$;$c + a$$0$;$c - b$$0$;
(2)化简:$|a - b|+|b + c|-|c + a|-|a - c|$。
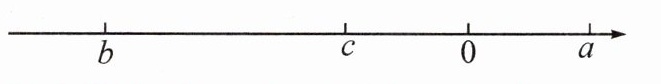
(1)填空:$a + b$$0$;$c + a$$0$;$c - b$$0$;
(2)化简:$|a - b|+|b + c|-|c + a|-|a - c|$。
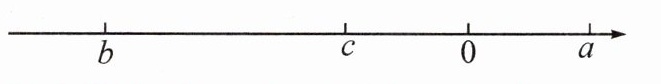
答案:
1. (1)
由数轴可知$b\lt c\lt0\lt a$,且$\vert a\vert=\vert c\vert$,$\vert b\vert\gt\vert a\vert$。
对于$a + b$:
根据有理数加法法则,异号两数相加,取绝对值较大的符号,$\vert b\vert\gt\vert a\vert$,$b\lt0$,所以$a + b\lt0$。
对于$c + a$:
因为$\vert a\vert=\vert c\vert$,$a$与$c$异号,根据互为相反数的两个数和为$0$,所以$c + a = 0$。
对于$c - b$:
$c - b=c+( - b)$,$c\gt0$,$-b\gt0$,根据有理数加法法则,同号两数相加,取相同的符号,所以$c - b\gt0$。
2. (2)
解:
因为$b\lt c\lt0\lt a$,$\vert a\vert=\vert c\vert$,$\vert b\vert\gt\vert a\vert$。
对于$\vert a - b\vert$:$a - b\gt0$,所以$\vert a - b\vert=a - b$。
对于$\vert b + c\vert$:$b + c\lt0$,所以$\vert b + c\vert=-(b + c)=-b - c$。
对于$\vert c + a\vert$:$c + a = 0$,所以$\vert c + a\vert = 0$。
对于$\vert a - c\vert$:$a - c=a+( - c)$,$a\gt0$,$-c\gt0$,$a - c\gt0$,$\vert a - c\vert=a - c$。
则$\vert a - b\vert+\vert b + c\vert-\vert c + a\vert-\vert a - c\vert=(a - b)+(-b - c)-0-(a - c)$。
去括号得:$a - b - b - c - a + c$。
合并同类项:$(a - a)+(-b - b)+(-c + c)=-2b$。
故答案为:(1)$\lt$,$=$,$\gt$;(2)$-2b$。
由数轴可知$b\lt c\lt0\lt a$,且$\vert a\vert=\vert c\vert$,$\vert b\vert\gt\vert a\vert$。
对于$a + b$:
根据有理数加法法则,异号两数相加,取绝对值较大的符号,$\vert b\vert\gt\vert a\vert$,$b\lt0$,所以$a + b\lt0$。
对于$c + a$:
因为$\vert a\vert=\vert c\vert$,$a$与$c$异号,根据互为相反数的两个数和为$0$,所以$c + a = 0$。
对于$c - b$:
$c - b=c+( - b)$,$c\gt0$,$-b\gt0$,根据有理数加法法则,同号两数相加,取相同的符号,所以$c - b\gt0$。
2. (2)
解:
因为$b\lt c\lt0\lt a$,$\vert a\vert=\vert c\vert$,$\vert b\vert\gt\vert a\vert$。
对于$\vert a - b\vert$:$a - b\gt0$,所以$\vert a - b\vert=a - b$。
对于$\vert b + c\vert$:$b + c\lt0$,所以$\vert b + c\vert=-(b + c)=-b - c$。
对于$\vert c + a\vert$:$c + a = 0$,所以$\vert c + a\vert = 0$。
对于$\vert a - c\vert$:$a - c=a+( - c)$,$a\gt0$,$-c\gt0$,$a - c\gt0$,$\vert a - c\vert=a - c$。
则$\vert a - b\vert+\vert b + c\vert-\vert c + a\vert-\vert a - c\vert=(a - b)+(-b - c)-0-(a - c)$。
去括号得:$a - b - b - c - a + c$。
合并同类项:$(a - a)+(-b - b)+(-c + c)=-2b$。
故答案为:(1)$\lt$,$=$,$\gt$;(2)$-2b$。
1. 有理数 $a,b$ 在数轴上的对应点的位置如图所示,则化简 $|a + b|+a$ 的结果是。
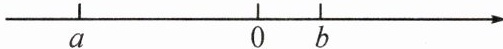
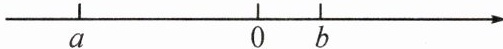
答案:
$-b$
2. 已知数 $a,b,c$ 在数轴上的对应点的位置如图所示,则化简 $|a|+|a + b|-|c|$ 的结果是。
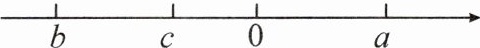
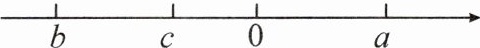
答案:
$c - b$
3. (2024·郑州四中期末)已知 $a,b,c$ 在数轴上的位置如图所示,则化简 $|a + c|-|a - 2b|-|c - 2b|$ 的结果是()

A.$0$
B.$4b$
C.$-2a - 2c$
D.$2a - 4b$

A.$0$
B.$4b$
C.$-2a - 2c$
D.$2a - 4b$
答案:
B
|代数式 $x^{2}+x+3$ 的值为 7,则代数式 $2x^{2}+2x - 3$ 的值为。|
|----|
【阅读理解】
小明在做作业时采用的方法如下:由题意,得 $x^{2}+x+3 = 7$,则 $x^{2}+x = 4$。所以 $2x^{2}+2x - 3 = 2(x^{2}+x)-3 = 2×4 - 3 = 5$。
【方法运用】
(1)若代数式 $x^{2}+x+1$ 的值为 15,求代数式 $-2x^{2}-2x+3$ 的值;
(2)当 $x = 2$ 时,代数式 $ax^{3}+bx+4$ 的值为 11,求当 $x = -2$ 时,代数式 $ax^{3}+bx+3$ 的值;
【拓展应用】
(3)若 $3m - 4n = -3$,$mn = -1$,求 $6(m - n)-2(n - mn)$ 的值。
【方法指导】
在代数式求值中,当单个字母的值不易求出或化简后的结果与已知值的式子相关联时,需要将已知式子的值整体代入计算。
|----|
【阅读理解】
小明在做作业时采用的方法如下:由题意,得 $x^{2}+x+3 = 7$,则 $x^{2}+x = 4$。所以 $2x^{2}+2x - 3 = 2(x^{2}+x)-3 = 2×4 - 3 = 5$。
【方法运用】
(1)若代数式 $x^{2}+x+1$ 的值为 15,求代数式 $-2x^{2}-2x+3$ 的值;
(2)当 $x = 2$ 时,代数式 $ax^{3}+bx+4$ 的值为 11,求当 $x = -2$ 时,代数式 $ax^{3}+bx+3$ 的值;
【拓展应用】
(3)若 $3m - 4n = -3$,$mn = -1$,求 $6(m - n)-2(n - mn)$ 的值。
【方法指导】
在代数式求值中,当单个字母的值不易求出或化简后的结果与已知值的式子相关联时,需要将已知式子的值整体代入计算。
答案:
(1)-25
(2)-4
(3)-8
(1)-25
(2)-4
(3)-8
1.(2024·南阳唐河县期中)已知 $a^{2}+3a - 4 = 0$,则代数式 $2a^{2}+6a - 11$ 的值为。
答案:
$-3$
2.(2024·南阳内乡县期末)若整式 $xy - 2y^{3}+2$ 的值为 5,则整式 $-3xy+6y^{3}-8$ 的值为。
答案:
-17
3. 当 $x = 1$ 时,$ax^{3}-bx - 5$ 的值是 2022,则当 $x = -1$ 时,$ax^{3}-bx - 5$ 的值是。
答案:
$-2032$(这里按题目要求应将答案放在对应位置,由于不是选择题,若按给定格式要求可理解为直接写出答案数值)故此处明确答案为$-2032$。
4.(2023·沈阳)当 $a + b = 3$ 时,代数式 $2(a + 2b)-(3a + 5b)+5$ 的值为。
答案:
2
查看更多完整答案,请扫码查看


