《2025年名校课堂七年级数学上册华师大版》

1. (1)把$(-2)× (-2)× (-2)× (-2)× (-2)$写成乘方的形式是；
(2)把$2^{5}$写成几个相同乘数的积的形式是。

答案：
(1)$(-2)^5$；
(2)$2 × 2 × 2 × 2 × 2$。

2. $(-9)^{8}$表示的意义是()

A.$-9$乘$8$
B.$8$个$-9$相乘的积
C.$9$个$8$相乘的积的相反数
D.$8$个$9$相乘的积的相反数

答案： B

3. 对于$-3^{4}$，下列叙述正确的是()

A.读作$-3$的$4$次幂
B.底数是$-3$，指数是$4$
C.表示$4$个$3$相乘的积的相反数
D.表示$4$个$-3$相乘的积

答案： C

4. 计算：
(1)$(-\frac{1}{2})^{2}=$；(2)$(-1)^{2024}=$。

答案：
(1) $\frac{1}{4}$
(2) $1$

5. 下列算式中，运算结果为负数的是()

A.$-(-5)$
B.$|-5|$
C.$(-5)^{2}$
D.$(-5)^{3}$

答案： D

6. 计算：
(1)$(-10)^{3}$；
(2)$(\frac{6}{5})^{2}$；
(3)$(-0.1)^{2}$；
(4)$(-1)^{4}× (-1)^{3}$。

答案：
(1)
$(-10)^{3}=(-10)× (-10)× (-10)= -1000$
(2)
$(\frac{6}{5})^{2}=\frac{6}{5}×\frac{6}{5}=\frac{36}{25}$
(3)
$(-0.1)^{2}=(-0.1)× (-0.1)= 0.01$
(4)
$(-1)^{4}× (-1)^{3}$
$=1× (-1)$
$=-1$

7. 老师出了一道计算题，计算：$(-2\frac{1}{3})^{3}$。
嘉嘉的计算过程如下：
解：原式$=(-2)^{3}× (\frac{1}{3})^{3}\cdots\cdots$第一步
$=(-8)× \frac{1}{27}\cdots\cdots$第二步
$=-\frac{8}{27}\cdots\cdots$第三步
(1)请问嘉嘉的计算过程是从第几步开始出错的？
(2)请把正确的计算过程写出来。

答案：
(1) 第一步。
(2) 解：
原式 = $(- \frac{7}{3})^{3}$
$= (-1)^{3} × (\frac{7}{3})^{3}$
$= - \frac{7^{3}}{3^{3}}$
$= - \frac{343}{27}$。

8. (2024·郑州新郑市期末)下列各组式子中，运算结果相同的是()

A.$-2^{3}$和$(-2)^{3}$
B.$-(-2)^{2}$与$2^{2}$
C.$(-2)^{2}$和$-2^{2}$
D.$|-2^{2}|$与$-|-2^{2}|$

答案： A

9. (2024·洛阳偃师区期末)已知$a$，$b$都是有理数，若$(a + 2)^{2}+|b - 1| = 0$，则$(a + b)^{2025}$的值是()

A.$-2025$
B.$-1$
C.$1$
D.$2025$

答案： B

10. 计算：
(1)$(-0.2)^{2}=$；
(2)$-(-5)^{3}=$；
(3)$(-\frac{1}{3})^{2}× (-\frac{1}{3})^{3}=$。

答案： 0.04；125；$-\frac{1}{243}$

11. 一种细胞，每经过$30$min 分裂一次，每次每个细胞分裂成$2$个，则$1$个细胞经过$3$h 能分裂成个。

答案： 64

12. 已知$3^{1}=3$，$3^{2}=9$，$3^{3}=27$，$3^{4}=81$，$3^{5}=243$，$\cdots$，那么$3^{2025}$的末位数字是。

答案： 3

13. 我们常用的数都是十进制数，如$2639 = 2× 10^{3}+6× 10^{2}+3× 10^{1}+9$。我国古代《易经》一书中记载，远古时期，人们通过在绳子上打结来记录数量，即“结绳计数”。一位母亲在从右到左依次排列的绳子上打结，采取满七进一的方式，用来记录孩子自出生后的天数。例如图 1 表示的是孩子出生后$30$天时打绳结的情况$(4× 7^{1}+2 = 30)$，那么图 2 表示的是孩子出生后天()


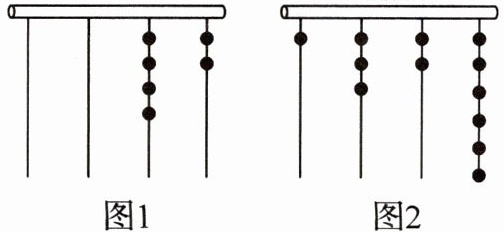
A.$520$
B.$513$
C.$511$
D.$510$

答案： D