《2025年名校课堂七年级数学上册华师大版》

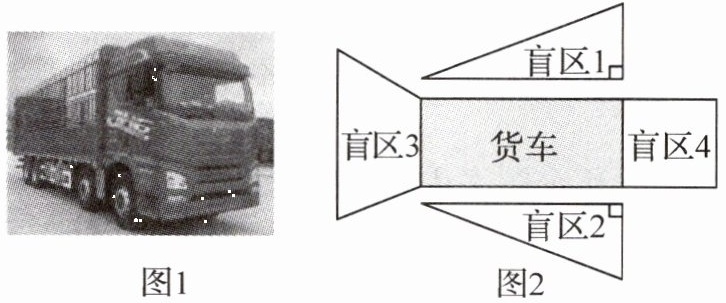
在一次普及“交通安全知识”的综合实践活动中，七年级学生们对货车（如图1）的盲区面积进行探究，得到货车盲区的部分分布图（如图2），盲区1与盲区2的面积相同，都是$\frac {3}{2}ab+a^{2}$，盲区3的面积是$-2ab+4a^{2}$，盲区4的面积是$a^{2}$.
（1）用含$a$，$b$的代数式表示图中盲区的总面积（结果需化简）；
（2）若$a=2$，$b=2$，求图中盲区的总面积.

答案： （1）$7a^2 + ab$；（2）$32$

2. (2023·南阳社旗县期末)某超市在春节期间对顾客实行优惠，规定如下：

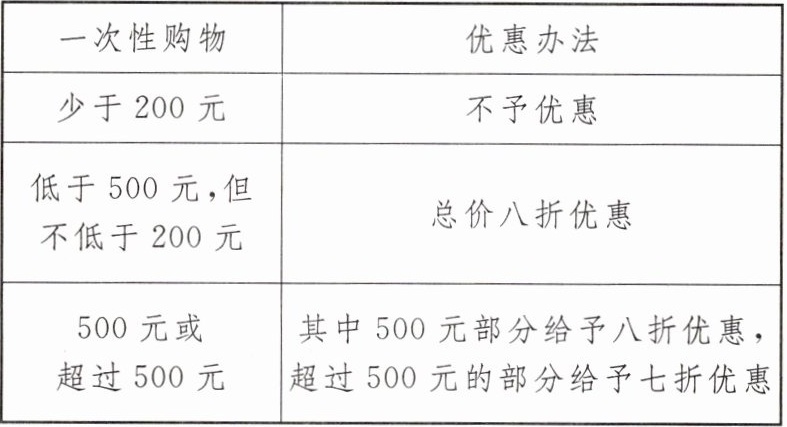
(1)周老师一次性购物400元，他实际付款元；
(2)若周老师在该超市一次性购物$x$元，当$x$小于500但不小于200时，他实际付款元；当$x$大于或等于500时，他实际付款元；(用含$x$的代数式表示)
(3)如果周老师两次购物货款合计880元，其中第一次购物的货款为 $ a(250 ＜ a ＜ 350) $ 元，求周老师两次购物实际一共付款多少元.（用含 $ a $ 的代数式表示）

答案： 1. （1）
因为$200\lt400\lt500$，根据优惠办法，总价八折优惠。
所以实际付款$400×0.8 = 320$元。
2. （2）
当$200\leq x\lt500$时：
根据优惠办法，总价八折优惠，所以实际付款$0.8x$元。
当$x\geq500$时：
$500$元部分给予八折优惠，这部分付款$500×0.8$元；超过$500$元的部分为$(x - 500)$元，这部分给予七折优惠，付款$0.7(x - 500)$元。
则实际付款$500×0.8+0.7(x - 500)=400 + 0.7x-350=(0.7x + 50)$元。
3. （3）
解：因为$250\lt a\lt350$，所以第一次购物实际付款$0.8a$元。
又因为两次购物货款合计$880$元，所以第二次购物货款为$(880 - a)$元，$880 - a=880-(250\lt a\lt350)$，则$530\lt880 - a\lt630$，即第二次购物货款大于$500$元。
第二次购物实际付款：
对于$880 - a$元，其中$500$元部分付款$500×0.8$元，超过$500$元的部分为$(880 - a - 500)=(380 - a)$元，这部分付款$0.7(380 - a)$元。
第二次购物实际付款$500×0.8+0.7(380 - a)=400+266-0.7a=(666 - 0.7a)$元。
两次购物实际一共付款：
$0.8a+(666 - 0.7a)$
$=0.8a+666 - 0.7a$
$=(0.1a + 666)$元。
综上，答案依次为：（1）$320$；（2）$0.8x$，$(0.7x + 50)$；（3）$(0.1a + 666)$元。

3. (2024·南阳内乡县期末)小语家新买了一套住房，其建筑平面图如图所示，其中 $ b ＜ a $(单位：m).
(1)这套住房的建筑总面积是 $ m^{2} $；(用含 $ a,b $ 的代数式表示)
(2)当 $ a = 5,b = 4 $ 时，求出小语家这套住房的总面积；
(3)地面装修要铺设地砖或地板，小语家对各个房间的装修都提出了具体要求，明确了选用材料的品牌以及规格、品质要求. 现有两家公司按照要求拿出了装修方案，两个方案中选用的材料品牌、规格、品质完全一致，但报价不同. 甲公司：客厅地面每平方米 240 元，书房和卧室地面每平方米 220 元，厨房地面每平方米 180 元，卫生间地面每平方米 150 元；乙公司：全屋地面每平方米 210 元. 请帮助小语家测算一下，选择哪家公司比较合算，并说明理由.

答案：
(1) $11a + 5b + 20$；
(2) $95$；
(3) 选择乙公司。