《2025年名校课堂七年级数学上册华师大版》

11. 某潜水员在水中作业时，先潜入水下$11.2m$，然后又上升了$8.5m$，这时潜水员处在什么位置？

答案： 设水面位置为$0$，潜入水下记为负，上升记为正。
潜水员先潜入水下$11.2m$，表示为$- 11.2m$。
然后又上升了$8.5m$，表示为$+ 8.5m$。
根据有理数的加法法则，潜水员当前位置为：
$( - 11.2) + ( + 8.5) = - 2.7（m）$。
所以，潜水员处在水下$2.7m$的位置。

12. 若$a$，$b$是有理数，则下列说法正确的是()

A.若$a＜0$，$b＜0$，则$a+b＞0$
B.若$a＞0$，$b＜0$，则$a+b＞0$
C.若$a＞0$，$b＜0$，则$a+b＜0$
D.若$a＜0$，$b＞0$，且$|a|＞|b|$，则$a+b＜0$

答案： D

13. 如图，在数轴上，点$A$，$B$表示的数分别是$a$，$b$，且$a+b=0$。若$A$，$B$两点的距离为$8$个单位长度，则$a$的值为()


A.$0$
B.$-8$
C.$4$
D.$-4$

答案： D

14. 填空：
(1)$(-9)+$$=9$；
(2)$12+$$=0$；
(3)$(-8)+$$=-15$；
(4)$7+$$=-6$。

答案：
(1) 18；
(2) -12；
(3) -7；
(4) -13。

15. 已知$|a|=1$，$b$是$2$的相反数，则$a+b$的值为。

答案： $-1$或$-3$（若为填空题，需分别填写两个值，根据题目要求格式，此处假设为多选或填写所有可能值，若为单选题则需调整，但根据题目开放形式，以完整解答为准。）

16. 在$1$，$-2$，$-3$这三个数中，任意两数之和的最大值是。

答案： -1

17. 计算：
(1)$-3+|-12|$；
(2)$-3.75+(-2\dfrac{1}{4})$。

答案：
(1)
首先计算绝对值 $|-12|$，由绝对值的定义，$|-12| = 12$。
然后计算 $-3 + 12$，根据有理数加法法则，$-3 + 12 = 9$。
(2)
首先将带分数 $-2\dfrac{1}{4}$ 转换为假分数，$-2\dfrac{1}{4} = -\dfrac{9}{4}$，或小数-2.25。
然后将 $-3.75$ 与 $-\dfrac{9}{4}$（或-2.25）相加，
根据有理数加法法则$-3.75 + (-2.25) = -3.75 - 2.25 = -6$。

18. 根据题意列式计算：
(1)比$-5$的相反数大$-10$的数；
(2)$15$的相反数与$-8$的绝对值的和。

答案：
(1)
首先，$-5$的相反数是$5$。
然后，比$5$大$-10$，即$5 + (-10)= -5$。
(2)
$15$的相反数是$-15$。
$-8$的绝对值是$8$。
它们的和为$-15 + 8 = -7$。

19. 下表是某水库一周内的水位变化情况，“$+$”表示水位比前一天上升，“$-$”表示水位比前一天下降，该水库的警戒水位是$32$米，已知上周周日的水位是$30$米。

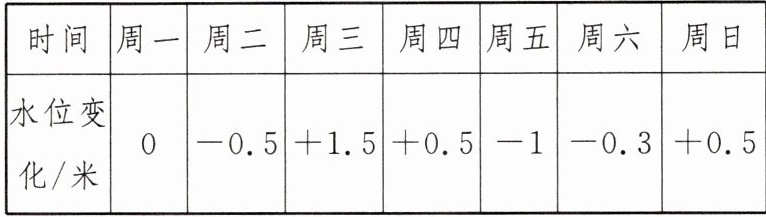
(1)小亮认为本周内周五的水位变化值为“$-1$”，所以这一天的水位最低，最低值为$29$米；小丽认为周五的水位变化值“$-1$”表示本周内周五的水位下降量最大，并不表示周五的水位最低。则(填“小亮”或“小丽”)的想法正确；
(2)本周哪一天该水库的水位最高？最高水位是否达到警戒水位？

答案：
(1) 小丽
(2) 计算每天水位：
周一：30 + 0 = 30米；
周二：30 + (-0.5) = 29.5米；
周三：29.5 + 1.5 = 31米；
周四：31 + 0.5 = 31.5米；
周五：31.5 + (-1) = 30.5米；
周六：30.5 + (-0.3) = 30.2米；
周日：30.2 + 0.5 = 30.7米。
本周周四水位最高，最高水位31.5米，31.5 ＜ 32，未达到警戒水位。