第25页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
8. 若四个有理数相乘,积为负数,则负因数的个数是()
A.1
B.2
C.3
D.1或3
A.1
B.2
C.3
D.1或3
答案:
D
9. (2023·南阳桐柏县期中)若三个连续非正整数的积是0,则这三个整数的和是()
A.-3
B.-2
C.0
D.3
A.-3
B.-2
C.0
D.3
答案:
A
10. 有理数$a$,$b$,$c$,$d$在数轴上的对应点的位置如图所示,则$abc$0,$abcd$0.(填“$>$”或“$<$”)
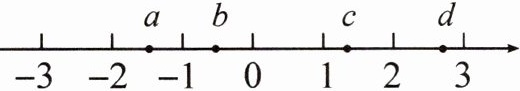
[img]
数轴上从左到右依次标有$-3$、$-2$、$a$、$-1$、$b$、$0$、$1$、$c$、$2$、$d$、$3$。
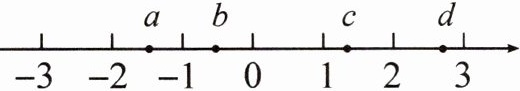
[img]
数轴上从左到右依次标有$-3$、$-2$、$a$、$-1$、$b$、$0$、$1$、$c$、$2$、$d$、$3$。
答案:
>,>
11. 绝对值小于6的所有负整数的积是。
答案:
$-120$
12. 计算:
(1)$(-1)×(-8)-9×(-1)×\frac{1}{3}$;
(2)$5×(-7)-(-5)×(-6)$;
(3)$(-8)×(-12)×(-0.125)×(-\frac{1}{3})×(-0.1)$;
(4)$2-(-2)×(-2)-(-2)×0×(-2)$。
(1)$(-1)×(-8)-9×(-1)×\frac{1}{3}$;
(2)$5×(-7)-(-5)×(-6)$;
(3)$(-8)×(-12)×(-0.125)×(-\frac{1}{3})×(-0.1)$;
(4)$2-(-2)×(-2)-(-2)×0×(-2)$。
答案:
(1)
$(-1)×(-8)-9×(-1)×\frac{1}{3}$
$=8 - (-3)$
$=8 + 3$
$=11$
(2)
$5×(-7)-(-5)×(-6)$
$=-35 - 30$
$=-65$
(3)
$(-8)×(-12)×(-0.125)×(-\frac{1}{3})×(-0.1)$
$=[(-8)×(-0.125)]×[(-12)×(-\frac{1}{3})]×(-0.1)$
$=1×4×(-0.1)$
$=-0.4$
(4)
$2-(-2)×(-2)-(-2)×0×(-2)$
$=2 - 4-0$
$=-2$
(1)
$(-1)×(-8)-9×(-1)×\frac{1}{3}$
$=8 - (-3)$
$=8 + 3$
$=11$
(2)
$5×(-7)-(-5)×(-6)$
$=-35 - 30$
$=-65$
(3)
$(-8)×(-12)×(-0.125)×(-\frac{1}{3})×(-0.1)$
$=[(-8)×(-0.125)]×[(-12)×(-\frac{1}{3})]×(-0.1)$
$=1×4×(-0.1)$
$=-0.4$
(4)
$2-(-2)×(-2)-(-2)×0×(-2)$
$=2 - 4-0$
$=-2$
13. (2023·信阳息县期中)定义一种新的运算“$*$”,规定:$a*b = 4ab$。例如:$2*3 = 4×2×3 = 24$。
(1)求$3*(-4)$的值;
(2)求$(-2)*(6*3)$的值。
(1)求$3*(-4)$的值;
(2)求$(-2)*(6*3)$的值。
答案:
(1)
根据新运算“$*$”的定义:$a*b = 4ab$,
则$3*(-4)=4×3×(-4)$
$=12×(-4)$
$=-48$
(2)
首先计算内层运算$6*3$:
$6*3 = 4×6×3$
$=72$
然后计算外层运算$(-2)*(6*3)$,即$(-2)*72$:
$(-2)*72=4×(-2)×72$
$=-8×72$
$=-576$
(1)
根据新运算“$*$”的定义:$a*b = 4ab$,
则$3*(-4)=4×3×(-4)$
$=12×(-4)$
$=-48$
(2)
首先计算内层运算$6*3$:
$6*3 = 4×6×3$
$=72$
然后计算外层运算$(-2)*(6*3)$,即$(-2)*72$:
$(-2)*72=4×(-2)×72$
$=-8×72$
$=-576$
14. 观察下列各式:
$\frac{1}{2}×\frac{2}{3}=\frac{1}{3}$;
$\frac{1}{2}×\frac{2}{3}×\frac{3}{4}=\frac{1}{4}$;
$\frac{1}{2}×\frac{2}{3}×\frac{3}{4}×\frac{4}{5}=\frac{1}{5}$;
……
(1)猜想:$\frac{1}{2}×\frac{2}{3}×\frac{3}{4}×…×\frac{59}{60}=$;
(2)根据上面的规律,计算:$(\frac{1}{100}-1)×(\frac{1}{99}-1)×(\frac{1}{98}-1)×…×(\frac{1}{2}-1)$。
$\frac{1}{2}×\frac{2}{3}=\frac{1}{3}$;
$\frac{1}{2}×\frac{2}{3}×\frac{3}{4}=\frac{1}{4}$;
$\frac{1}{2}×\frac{2}{3}×\frac{3}{4}×\frac{4}{5}=\frac{1}{5}$;
……
(1)猜想:$\frac{1}{2}×\frac{2}{3}×\frac{3}{4}×…×\frac{59}{60}=$;
(2)根据上面的规律,计算:$(\frac{1}{100}-1)×(\frac{1}{99}-1)×(\frac{1}{98}-1)×…×(\frac{1}{2}-1)$。
答案:
(1)
观察所给式子可发现规律:$\frac{1}{2}×\frac{2}{3}×\frac{3}{4}×\cdots×\frac{n}{n + 1}=\frac{1}{n + 1}$。
当$n = 59$时,$\frac{1}{2}×\frac{2}{3}×\frac{3}{4}×\cdots×\frac{59}{60}=\frac{1}{60}$。
(2)
先对$(\frac{1}{n}-1)$进行化简,$\frac{1}{n}-1=\frac{1 - n}{n}=-\frac{n - 1}{n}$。
则$(\frac{1}{100}-1)×(\frac{1}{99}-1)×(\frac{1}{98}-1)×\cdots×(\frac{1}{2}-1)$
$=-\frac{99}{100}×(-\frac{98}{99})×(-\frac{97}{98})×\cdots×(-\frac{1}{2})$
一共有$100 - 2+1 = 99$个负数相乘,结果为负。
根据乘法法则可得:$-\frac{1}{100}$。
综上,答案依次为:
(1)$\frac{1}{60}$;
(2)$-\frac{1}{100}$。
(1)
观察所给式子可发现规律:$\frac{1}{2}×\frac{2}{3}×\frac{3}{4}×\cdots×\frac{n}{n + 1}=\frac{1}{n + 1}$。
当$n = 59$时,$\frac{1}{2}×\frac{2}{3}×\frac{3}{4}×\cdots×\frac{59}{60}=\frac{1}{60}$。
(2)
先对$(\frac{1}{n}-1)$进行化简,$\frac{1}{n}-1=\frac{1 - n}{n}=-\frac{n - 1}{n}$。
则$(\frac{1}{100}-1)×(\frac{1}{99}-1)×(\frac{1}{98}-1)×\cdots×(\frac{1}{2}-1)$
$=-\frac{99}{100}×(-\frac{98}{99})×(-\frac{97}{98})×\cdots×(-\frac{1}{2})$
一共有$100 - 2+1 = 99$个负数相乘,结果为负。
根据乘法法则可得:$-\frac{1}{100}$。
综上,答案依次为:
(1)$\frac{1}{60}$;
(2)$-\frac{1}{100}$。
查看更多完整答案,请扫码查看


