第7页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
13. 若$-a$的相反数是$-5$,则$a=$.
答案:
-5
14. 一个数的相反数比它本身大,则这个数是()
A.正数
B.负数
C.$0$
D.负数和$0$
A.正数
B.负数
C.$0$
D.负数和$0$
答案:
B
15. (2023·信阳平桥区开学考)在$-2\frac{1}{2}$和它的相反数之间的整数个数为()
A.$3$
B.$4$
C.$5$
D.$6$
A.$3$
B.$4$
C.$5$
D.$6$
答案:
C
16. (2024·南阳期中)下列各对数中,互为相反数的是()
A.$+(-2.5)$和$-2\frac{1}{2}$
B.$-(+4\frac{1}{3})$和$+(-4\frac{1}{3})$
C.$-(-1.8)$和$+(-1.8)$
D.$-(-2)$和$+(+2)$
A.$+(-2.5)$和$-2\frac{1}{2}$
B.$-(+4\frac{1}{3})$和$+(-4\frac{1}{3})$
C.$-(-1.8)$和$+(-1.8)$
D.$-(-2)$和$+(+2)$
答案:
C
17. 如图所示,已知$A$,$B$,$C$,$D$四个点在一条没有标明原点的数轴上,点$A$与点$B$的距离为$2$个单位长度,点$A$与点$C$的距离为$4$个单位长度,点$A$与点$D$的距离为$6$个单位长度.
(1)若点$A$和点$C$表示的数互为相反数,则原点为点;
(2)若点$B$和点$D$表示的数互为相反数,则原点为点;
(3)若点$A$和点$D$表示的数互为相反数,请在数轴上标出原点$O$的位置,此时点$B$表示的数是,点$C$表示的数(填“是”或“不是”)点$B$表示的数的相反数.

(1)若点$A$和点$C$表示的数互为相反数,则原点为点;
(2)若点$B$和点$D$表示的数互为相反数,则原点为点;
(3)若点$A$和点$D$表示的数互为相反数,请在数轴上标出原点$O$的位置,此时点$B$表示的数是,点$C$表示的数(填“是”或“不是”)点$B$表示的数的相反数.

答案:
(1)B
(2)C
(3)-1;是
(1)B
(2)C
(3)-1;是
18. (1)化简下列各数:
①$-[-(+1)]$; ②$-[-(-1)]$;
③$-\{ -[-(+1)]\}$; ④$-\{ -[-(-1)]\}$;
(2)若化简的数不为$0$,则化简过程中先省略所有的“$+$”,再观察原式中的“$-$”的个数,当“$-$”的个数是奇数时,化简结果为数;当“$-$”的个数是偶数时,化简结果为数.
①$-[-(+1)]$; ②$-[-(-1)]$;
③$-\{ -[-(+1)]\}$; ④$-\{ -[-(-1)]\}$;
(2)若化简的数不为$0$,则化简过程中先省略所有的“$+$”,再观察原式中的“$-$”的个数,当“$-$”的个数是奇数时,化简结果为数;当“$-$”的个数是偶数时,化简结果为数.
答案:
(1)
①$-[-(+1)]= -(-1)=1$;
②$-[-(-1)]=-(1)= -1$;
③$-\{ -[-(+1)]\}=-\{ -(-1)\}=-(1)= -1$;
④$-\{ -[-(-1)]\}=-\{ -(1)\}=-(-1)=1$;
(2)负;正。
(1)
①$-[-(+1)]= -(-1)=1$;
②$-[-(-1)]=-(1)= -1$;
③$-\{ -[-(+1)]\}=-\{ -(-1)\}=-(1)= -1$;
④$-\{ -[-(-1)]\}=-\{ -(1)\}=-(-1)=1$;
(2)负;正。
19. 操作与分析
【特例呈现】已知有理数$a$,$b$在没有标明单位长度的数轴上的对应点的大致位置如图所示:
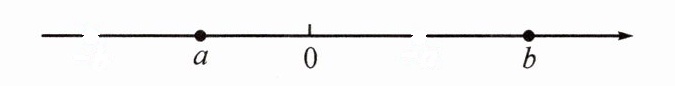
【操作应用】
(1)在数轴上标出$a$,$b$的相反数$-a$,$-b$的对应点的位置;
【初步分析】
(2)若表示数$a$与$-a$的点相隔$2024$个单位长度,则数$a$是多少?
【拓展探究】
(3)在(2)的条件下,若数$a$对应的点与数$b$的相反数对应的点相距$5$个单位长度,则$b=$.
【特例呈现】已知有理数$a$,$b$在没有标明单位长度的数轴上的对应点的大致位置如图所示:
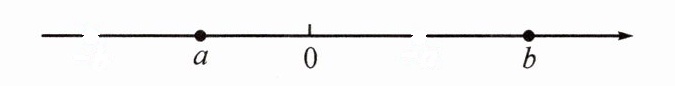
【操作应用】
(1)在数轴上标出$a$,$b$的相反数$-a$,$-b$的对应点的位置;
【初步分析】
(2)若表示数$a$与$-a$的点相隔$2024$个单位长度,则数$a$是多少?
【拓展探究】
(3)在(2)的条件下,若数$a$对应的点与数$b$的相反数对应的点相距$5$个单位长度,则$b=$.
答案:
(1) 因为a是负数,所以-a是正数,在原点右边,与a到原点距离相等;b是正数,所以-b是负数,在原点左边,与b到原点距离相等。
(2) 因为a与-a互为相反数,两点间距离为2|a|,由2|a|=2024,得|a|=1012,又a是负数,所以a=-1012。
(3) a=-1012,数a对应的点与-b对应的点相距5个单位,即|-1012 - (-b)|=5,|b - 1012|=5,所以b=1012±5,即b=1017或1007。结合数轴上b在原点右边且位置,b=1007。
1007
(1) 因为a是负数,所以-a是正数,在原点右边,与a到原点距离相等;b是正数,所以-b是负数,在原点左边,与b到原点距离相等。
(2) 因为a与-a互为相反数,两点间距离为2|a|,由2|a|=2024,得|a|=1012,又a是负数,所以a=-1012。
(3) a=-1012,数a对应的点与-b对应的点相距5个单位,即|-1012 - (-b)|=5,|b - 1012|=5,所以b=1012±5,即b=1017或1007。结合数轴上b在原点右边且位置,b=1007。
1007
查看更多完整答案,请扫码查看


