《2025年名校课堂七年级数学上册华师大版》

1. 使用计算器时，下列按键顺序正确的是()

A.$5×(-8)$：$\boxed{5}\boxed{×}\boxed{(-)}\boxed{8}\boxed{EXE}$
B.$(-8)×5$：$\boxed{8}\boxed{(-)}\boxed{×}\boxed{5}\boxed{EXE}$
C.$3 + 4.9÷7$：$\boxed{3}\boxed{+}\boxed{4}\boxed{9}\boxed{÷}\boxed{7}\boxed{EXE}$
D.$26×(-0.3)$：$\boxed{2}\boxed{6}\boxed{×}\boxed{.}\boxed{3}\boxed{(-)}\boxed{EXE}$

答案： A

2. 在计算器上依次按键$\boxed{9}\boxed{0}\boxed{÷}\boxed{6}\boxed{-}\boxed{1}\boxed{3}\boxed{.}\boxed{4}\boxed{×}\boxed{2}\boxed{EXE}\boxed{格式}\boxed{▼}\boxed{EXE}$后，显示的结果为。

答案： $-11.8$（由于本题为计算题，答案应以具体数值填写）

3. 用科学计算器求$5^{3}$的值，按键顺序是()

答案： D

4. 利用计算器，按照下列步骤按键，显示结果为()


A.$-10$
B.$-32$
C.$-2.5$
D.$-7$

答案： B

5. 小王利用计算机设计了一个计算程序，输入和输出的数据如下表：

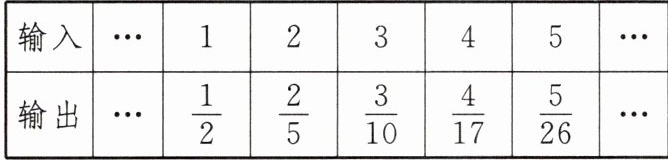
那么当输入数据为$8$时，输出的数据为()

A.$\dfrac{8}{63}$
B.$\dfrac{8}{67}$
C.$\dfrac{8}{65}$
D.$\dfrac{8}{61}$

答案： C

6. 用计算器计算：
(1) $-3.7^{3}+(-3.8)^{4}$（精确到$0.01$）；
(2) $[6.38÷(-2)+6.5^{3}]×17.3$（精确到百位）。

答案：
(1)
首先使用计算器计算$-3.7^{3}$：
$-3.7^{3}=-3.7×3.7×3.7 = - 50.653$
然后计算$(-3.8)^{4}$：
$(-3.8)^{4}=3.8×3.8×3.8×3.8 = 208.5136$
则$-3.7^{3}+(-3.8)^{4}=-50.653 + 208.5136=157.8606\approx157.86$
(2)
先计算$6.38÷(-2)$：
$6.38÷(-2)=-3.19$
再计算$6.5^{3}$：
$6.5^{3}=6.5×6.5×6.5 = 274.625$
则$6.38÷(-2)+6.5^{3}=-3.19 + 274.625 = 271.435$
所以$[6.38÷(-2)+6.5^{3}]×17.3=271.435×17.3$
$271.435×17.3 = 4695.8255\approx4.7×10^{3}$
综上，答案依次为：
(1)$157.86$；
(2)$4.7×10^{3}$。

7. 利用计算器计算：一张纸的厚度大约是$0.1$毫米，将它对折$30$次后，将它的厚度与珠穆朗玛峰的高度比较一下（珠峰高$8848$米），看谁更高（是不是吓你一大跳，请注意单位换算）。

答案： 1. 计算对折30次后的厚度：每次对折厚度翻倍，对折30次后厚度为 $0.1 × 2^{30}$ 毫米。
2. 使用计算器计算 $2^{30} = 1073741824$。
3. 厚度 = $0.1 × 1073741824 = 107374182.4$ 毫米。
4. 单位换算：107374182.4 毫米 = 107374.1824 米。
5. 比较：107374.1824 米 ＞ 8848 米。
结论：对折30次后的厚度更高。

8.用计算器探索：
(1) 用计算器计算下列各式：$34×34$，$334×334$，$3334×3334$，$33334×33334$；
(2) 根据(1)中的计算结果，你发现了什么规律？
(3) 不用计算器，试直接写出$3333334×3333334$的结果。

答案：
(1) $34×34 = 1156$，$334×334 = 111556$，$3334×3334 = 11115556$，$33334×33334 = 1111155556$；
(2) 规律：两个因数都由$n$个$3$和一个$4$组成（$n\geq1$），积由$(n + 1)$个$1$、$n$个$5$和一个$6$组成；
(3) $111111555556$