3. 计算(结果保留两位小数):
(1) $2\sqrt{3}-3\sqrt{3}+\frac{5}{6}\sqrt{3}-\frac{1}{2}\sqrt{3}$;
(2) $(\frac{\sqrt{5}}{3})^{3}×\sqrt{3}×\sqrt{5}$;
(3) $\sqrt{(-\frac{1}{4})^{-2}+(\sqrt{10})^{2}}$;
(4) $(\sqrt{2})^{3}+(\sqrt{2}×\sqrt{3})^{2}$.
(1) $2\sqrt{3}-3\sqrt{3}+\frac{5}{6}\sqrt{3}-\frac{1}{2}\sqrt{3}$;
(2) $(\frac{\sqrt{5}}{3})^{3}×\sqrt{3}×\sqrt{5}$;
(3) $\sqrt{(-\frac{1}{4})^{-2}+(\sqrt{10})^{2}}$;
(4) $(\sqrt{2})^{3}+(\sqrt{2}×\sqrt{3})^{2}$.
答案:
3.(1)$-\dfrac{2}{3}\sqrt{3}\approx-1.15$.(2)$\dfrac{25}{27}\sqrt{3}\approx1.60$.(3)$\sqrt{26}\approx5.10$.(4)$2\sqrt{2}+6\approx8.83$.
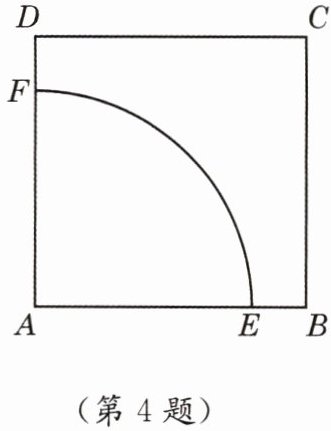
4. 如图,某公园里有一块边长为 10 m 的正方形绿地(如图所示的正方形 ABCD),在绿地中划出一块区域(扇形 EAF)举办花展. 若花展区域面积占正方形绿地面积的一半,求 AF 的长(π 取 3.14,结果精确到 0.1 m).

答案:
4. $AF$的长为$8.0\ m$.
查看更多完整答案,请扫码查看


