3. 用计算器求值(近似值保留两位小数),并在如图所示的数轴上标出其所对应的点的大致位置:
(1)$\sqrt[3]{-10}与\sqrt{0.5}$;

(2)$-\sqrt[3]{128}与-\sqrt{24}$.

(1)$\sqrt[3]{-10}与\sqrt{0.5}$;

(2)$-\sqrt[3]{128}与-\sqrt{24}$.

答案:
3.
(1)$\sqrt[3]{-10}$≈ -2.15,$\sqrt{0.5}$≈0.71,数轴略.
(2)$-\sqrt[3]{128}$≈ -5.04,$-\sqrt{24}$≈ -4.90,数轴略.
(1)$\sqrt[3]{-10}$≈ -2.15,$\sqrt{0.5}$≈0.71,数轴略.
(2)$-\sqrt[3]{128}$≈ -5.04,$-\sqrt{24}$≈ -4.90,数轴略.
4. 如图,点 $E$ 在数轴上表示数 $1$,以 $E$ 为直角顶点,$EO$ 为一直角边,在数轴的上方画一个等腰直角三角形 $OEF$,那么 $OF = \sqrt{2}$. 回答下列问题:
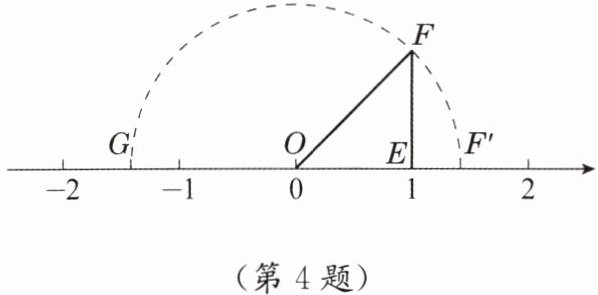
(1)在数轴的正半轴上截取 $OF' = OF$,则点 $F'$ 表示的实数是
(2)在数轴的负半轴上截取 $OG = OF$,则点 $G$ 表示的实数是

(1)在数轴的正半轴上截取 $OF' = OF$,则点 $F'$ 表示的实数是
$\sqrt{2}$
;(2)在数轴的负半轴上截取 $OG = OF$,则点 $G$ 表示的实数是
$-\sqrt{2}$
.
答案:
4.
(1)$\sqrt{2}$
(2)$-\sqrt{2}$
(1)$\sqrt{2}$
(2)$-\sqrt{2}$
查看更多完整答案,请扫码查看


