《2025年高分突破课时达标讲练测九年级物理全一册沪科版》

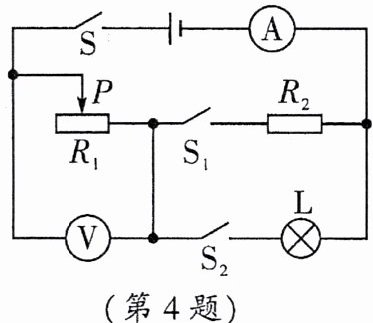
4. (2025·西附)如图所示电路,电源电压恒为6 V保持不变,小灯泡L标有“5 V 0.4 A”字样(灯丝电阻不变),滑动变阻器$R_1$的铭牌是“20 Ω 1 A”,电流表的量程是0~0.6 A,电压表的量程是0~3 V。求:
(1)小灯泡正常发光时的电阻;
(2)只闭合开关S和$S_1,$滑动变阻器的滑片P置于某一位置时,电压表的示数为1 V,电流表的示数为0.2 A,求定值电阻$R_2$的阻值;
(3)只闭合开关S和$S_2,$移动滑动变阻器的滑片P,在保证电路各元件安全工作的情况下,滑动变阻器的取值范围。

答案： 【解析】：
本题主要考查了欧姆定律、电功率公式以及串联电路的特点，同时结合了电路的动态分析，需要考虑电表的量程以及用电器的规格等条件来确定滑动变阻器的取值范围。
（1）已知小灯泡的额定电压和额定电流，根据欧姆定律$I = \frac{U}{R}$的变形公式$R=\frac{U}{I}$，可求出小灯泡正常发光时的电阻。
（2）只闭合开关$S$和$S_1$时，$R_1$与$R_2$串联，电压表测$R_1$两端的电压，电流表测电路中的电流。根据串联电路的电压特点求出$R_2$两端的电压，再利用欧姆定律求出$R_2$的阻值。
（3）只闭合开关$S$和$S_2$时，$L$与$R_1$串联，电压表测$R_1$两端的电压，电流表测电路中的电流。
先根据小灯泡的额定电流和电流表的量程确定电路中的最大电流，此时滑动变阻器接入电路的电阻最小，根据串联电路的特点和欧姆定律求出滑动变阻器接入电路的最小阻值。
再根据电压表的量程确定滑动变阻器两端的最大电压，此时滑动变阻器接入电路的电阻最大，根据串联电路的特点和欧姆定律求出滑动变阻器接入电路的最大阻值。
【答案】：
（1）由$I = \frac{U}{R}$可得，小灯泡正常发光时的电阻：$R_{L}=\frac{U_{L}}{I_{L}}=\frac{5V}{0.4A}=12.5\Omega$。
（2）只闭合开关$S$和$S_1$时，$R_1$与$R_2$串联，电压表测$R_1$两端的电压，电流表测电路中的电流。
因串联电路中总电压等于各分电压之和，所以，$R_2$两端的电压：$U_{2}=U - U_{1}=6V - 1V = 5V$，由$I = \frac{U}{R}$可得，定值电阻$R_2$的阻值：$R_{2}=\frac{U_{2}}{I}=\frac{5V}{0.2A}=25\Omega$。
（3）只闭合开关$S$和$S_2$时，$L$与$R_1$串联，电压表测$R_1$两端的电压，电流表测电路中的电流。
由小灯泡的额定电流为$0.4A$，电流表的量程为$0\sim0.6A$，滑动变阻器允许通过的最大电流为$1A$，所以，电路中的最大电流$I_{大}=0.4A$，此时滑动变阻器接入电路的电阻最小。
此时电路的总电阻：$R_{总}=\frac{U}{I_{大}}=\frac{6V}{0.4A}=15\Omega$，因串联电路中总电阻等于各分电阻之和，所以，滑动变阻器接入电路的最小阻值：$R_{1小}=R_{总}-R_{L}=15\Omega - 12.5\Omega = 2.5\Omega$。
当电压表的示数$U_{1大}=3V$时，滑动变阻器接入电路的电阻最大，因串联电路中总电压等于各分电压之和，所以，灯泡两端的电压：$U_{L小}=U - U_{1大}=6V - 3V = 3V$，此时电路中的电流：$I_{小}=\frac{U_{L小}}{R_{L}}=\frac{3V}{12.5\Omega}=0.24A$，则滑动变阻器接入电路的最大阻值：$R_{1大}=\frac{U_{1大}}{I_{小}}=\frac{3V}{0.24A}=12.5\Omega$。
所以，滑动变阻器的取值范围是$2.5\Omega\sim12.5\Omega$。

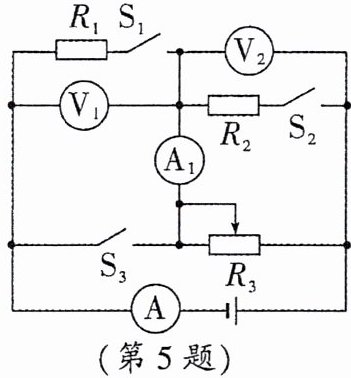
5. 如图所示,电源电压为$12 V,R_1、$$R_2$为定值电阻$,R_2= 20 Ω,R_3$为滑动变阻器,其铭牌上标有“? Ω 2 A”字样。将滑动变阻器$R_3$的滑片调至最左端,当只闭合开关$S_3$时,电流表A的示数为0.4 A;保持滑片位置不变,当只闭合开关$S_1$时,电压表$V_1$的示数为3 V。求:
(1)滑动变阻器$R_3$的最大阻值;
$(2)R_1$的阻值;
(3)电压表$V_1$接入电路的量程为0~3 V,电压表$V_2$接入电路的量程为0~15 V,电流表A所选量程为0~3 A,电流表$A_1$所选量程为0~0.6 A。通过改变电路的连接情况,在保障各电路元件安全的情况下,电流表A的最大示数和最小示数之比。

答案：
(1)解：只闭合S₃时，R₃单独接入电路，滑片在最左端，R₃连入最大阻值。
由I=U/R得，R₃最大阻值R₃=U/I=12V/0.4A=30Ω。
(2)解：保持滑片位置不变（R₃=30Ω），只闭合S₁时，R₁与R₃串联，V₁测R₁电压U₁=3V。
电路中电流I'=I₁=I₃=(U-U₁)/R₃=(12V-3V)/30Ω=0.3A。
R₁=U₁/I₁=3V/0.3A=10Ω。
(3)解：
最大示数：S₁、S₂、S₃都闭合时，R₁与R₂并联，R₃被短路。
I₁=U/R₁=12V/10Ω=1.2A（A₁测R₁电流，1.2A＞0.6A，A₁超量程，此情况不成立）。
只闭合S₂、S₃时，R₂与R₃并联，R₂=20Ω，I₂=U/R₂=12V/20Ω=0.6A。R₃滑片调至最小阻值（0Ω），I₃=U/R₃'，R₃'最小，I₃最大，干路电流I=I₂+I₃。R₃允许最大电流2A，I₃=2A，I=0.6A+2A=2.6A（A量程0 - 3A，安全）。
最小示数：R₁、R₂、R₃串联，S₁、S₂闭合，S₃断开，滑片调至最大阻值R₃=30Ω。
总电阻R=R₁+R₂+R₃=10Ω+20Ω+30Ω=60Ω，I小=U/R=12V/60Ω=0.2A。
最大示数2.6A，最小示数0.2A，比值2.6A:0.2A=13:1。
答：
(1)30Ω；
(2)10Ω；
(3)13:1。