第27页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
9. (2024·安徽)一保温杯中装有质量为200g,温度为25℃的水。将一个质量为100g、温度为100℃的金属块放入杯中,一段时间后杯内水和金属块的温度稳定在30℃,假设金属块放出的热量全部被水吸收,已知水的比热容为$4.2×10^3J/(kg·℃),$则该金属块的比热容为
$0.6×10^{3}$
J/(kg·℃)。
答案:
解:已知水的质量$m_{水}=200g=0.2kg$,初温$t_{0水}=25℃$,末温$t=30℃$,比热容$c_{水}=4.2×10^{3}J/(kg·℃)$;金属块质量$m_{金}=100g=0.1kg$,初温$t_{0金}=100℃$。
水吸收的热量:$Q_{吸}=c_{水}m_{水}(t - t_{0水})=4.2×10^{3}J/(kg·℃)×0.2kg×(30℃ - 25℃)=4200J$。
金属块放出的热量$Q_{放}=Q_{吸}=4200J$。
由$Q_{放}=c_{金}m_{金}(t_{0金}-t)$得,金属块的比热容:$c_{金}=\frac{Q_{放}}{m_{金}(t_{0金}-t)}=\frac{4200J}{0.1kg×(100℃ - 30℃)}=0.6×10^{3}J/(kg·℃)$。
答案:$0.6×10^{3}$
水吸收的热量:$Q_{吸}=c_{水}m_{水}(t - t_{0水})=4.2×10^{3}J/(kg·℃)×0.2kg×(30℃ - 25℃)=4200J$。
金属块放出的热量$Q_{放}=Q_{吸}=4200J$。
由$Q_{放}=c_{金}m_{金}(t_{0金}-t)$得,金属块的比热容:$c_{金}=\frac{Q_{放}}{m_{金}(t_{0金}-t)}=\frac{4200J}{0.1kg×(100℃ - 30℃)}=0.6×10^{3}J/(kg·℃)$。
答案:$0.6×10^{3}$
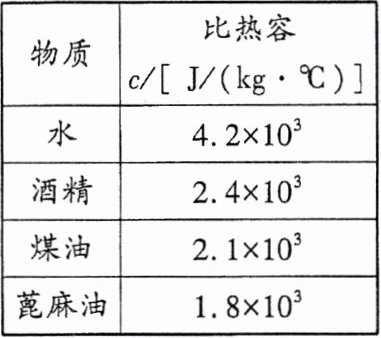
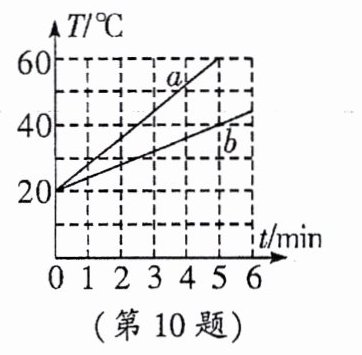
10. (2024·烟台)在探究“物质的吸热能力与哪些因素有关”的实验中,用质量是0.3kg的水和表中等质量的另一种物质进行对比,作出的图像如图所示。实验过程中,水和另一种物质在相同时间内吸收的热量相等,分析图像可以得出图线______(选填“a”或“b”)对应的物质为水,另一种物质为______,这种物质在0~5min内吸收的热量为______J。
|物质|比热容c/[J/(kg·℃)]|
|水|$4.2×10^3$|
|酒精|$2.4×10^3$|
|煤油|$2.1×10^3$|
|蓖麻油|$1.8×10^3$|
|物质|比热容c/[J/(kg·℃)]|
|水|$4.2×10^3$|
|酒精|$2.4×10^3$|
|煤油|$2.1×10^3$|
|蓖麻油|$1.8×10^3$|


a;煤油;$2.52×10^4$
答案:
【解析】:
本题考查的是对比热容的理解及吸放热公式的应用。我们需要通过图像判断哪种物质是水,并计算另一种物质在0到5分钟内吸收的热量。
实验中水和另一种物质的质量相同,在相同时间内吸收的热量相等,
由图可知,在相同时间内(吸热相同),a物质的温度升高得慢;b物质的温度升高得快,
根据比热容的定义,质量相同的物质,吸收相同的热量,温度升高得慢则比热容大,
所以a物质的比热容大,由表格数据可知a物质是水,b物质是煤油;
读图可知,在0到5分钟内,水升高的温度是$50^{\circ}C-30^{\circ}C=20^{\circ}C$,
煤油升高的温度是$50^{\circ}C-10^{\circ}C=40^{\circ}C$,
根据吸热公式$Q=cm\Delta t$,且水和煤油吸收的热量相等,
可列等式:$4.2×10^3×0.3×20=2.1×10^3×m×40$,
解得:$m=0.3kg$,
所以煤油在0到5分钟内吸收的热量为:$Q=cm\Delta t=2.1×10^3×0.3×40=2.52×10^4$J。
【答案】:
a;煤油;$2.52×10^4$。
本题考查的是对比热容的理解及吸放热公式的应用。我们需要通过图像判断哪种物质是水,并计算另一种物质在0到5分钟内吸收的热量。
实验中水和另一种物质的质量相同,在相同时间内吸收的热量相等,
由图可知,在相同时间内(吸热相同),a物质的温度升高得慢;b物质的温度升高得快,
根据比热容的定义,质量相同的物质,吸收相同的热量,温度升高得慢则比热容大,
所以a物质的比热容大,由表格数据可知a物质是水,b物质是煤油;
读图可知,在0到5分钟内,水升高的温度是$50^{\circ}C-30^{\circ}C=20^{\circ}C$,
煤油升高的温度是$50^{\circ}C-10^{\circ}C=40^{\circ}C$,
根据吸热公式$Q=cm\Delta t$,且水和煤油吸收的热量相等,
可列等式:$4.2×10^3×0.3×20=2.1×10^3×m×40$,
解得:$m=0.3kg$,
所以煤油在0到5分钟内吸收的热量为:$Q=cm\Delta t=2.1×10^3×0.3×40=2.52×10^4$J。
【答案】:
a;煤油;$2.52×10^4$。
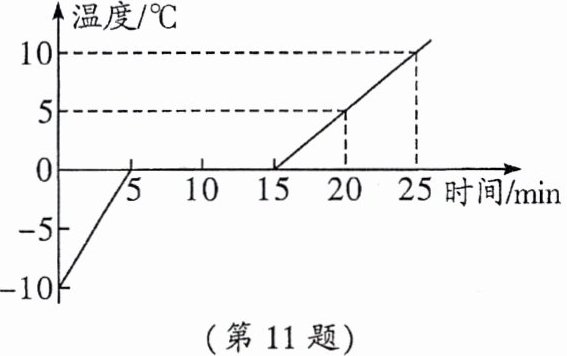
11. (2025·巴蜀)如图所示,用同一酒精灯加热使50g冰熔化成水,将实验数据绘制成温度随时间变化的图像(假设在加热过程中物质的质量不变,单位时间内吸收的热量相同),根据图中信息,算出c冰:c水=
1:2
,冰在熔化过程中吸收了2.1×10³
J的热量。[c水$= 4.2×10^3J/(kg·℃)]$
答案:
【解析】:本题可根据图像获取冰和水升温的时间,结合单位时间内吸收热量相同,利用热量公式$Q = cm\Delta t$求出冰和水的比热容之比;再根据水升温吸收的热量以及冰熔化时间与水升温时间的关系求出冰在熔化过程中吸收的热量。
1. 求$c_{冰}:c_{水}$的值:
由图像可知,冰从$- 10^{\circ}C$升高到$0^{\circ}C$用时$5min$,水从$0^{\circ}C$升高到$10^{\circ}C$用时$10min$。
因为单位时间内吸收的热量相同,设单位时间内吸收的热量为$Q_0$,则冰吸收的热量$Q_{冰}=Q_0×5$,水吸收的热量$Q_{水}=Q_0×10$。
根据热量公式$Q = cm\Delta t$(其中$Q$为吸收的热量,$c$为比热容,$m$为质量,$\Delta t$为温度变化量),冰的质量$m_{冰}=m_{水}=50g = 0.05kg$,冰的温度变化量$\Delta t_{冰}=0^{\circ}C - (-10^{\circ}C)=10^{\circ}C$,水的温度变化量$\Delta t_{水}=10^{\circ}C - 0^{\circ}C = 10^{\circ}C$。
对于冰有$Q_{冰}=c_{冰}m_{冰}\Delta t_{冰}$,即$Q_0×5 = c_{冰}×0.05kg×10^{\circ}C$ ①;对于水有$Q_{水}=c_{水}m_{水}\Delta t_{水}$,即$Q_0×10 = c_{水}×0.05kg×10^{\circ}C$ ②。
用①$÷$②可得:$\frac{Q_0×5}{Q_0×10}=\frac{c_{冰}×0.05kg×10^{\circ}C}{c_{水}×0.05kg×10^{\circ}C}$,化简得$\frac{c_{冰}}{c_{水}}=\frac{1}{2}$。
2. 求冰在熔化过程中吸收的热量:
由图像可知,冰熔化过程用时$15min - 5min = 10min$,水从$0^{\circ}C$升高到$10^{\circ}C$用时$10min$。
水吸收的热量$Q_{水吸}=c_{水}m_{水}\Delta t_{水}=4.2×10^{3}J/(kg\cdot^{\circ}C)×0.05kg×(10^{\circ}C - 0^{\circ}C)=2.1×10^{3}J$。
因为单位时间内吸收的热量相同,且冰熔化时间与水升温时间相同,所以冰在熔化过程中吸收的热量$Q_{熔化}=Q_{水吸}=2.1×10^{3}J$。
【答案】:$1:2$;$2.1×10^3$
1. 求$c_{冰}:c_{水}$的值:
由图像可知,冰从$- 10^{\circ}C$升高到$0^{\circ}C$用时$5min$,水从$0^{\circ}C$升高到$10^{\circ}C$用时$10min$。
因为单位时间内吸收的热量相同,设单位时间内吸收的热量为$Q_0$,则冰吸收的热量$Q_{冰}=Q_0×5$,水吸收的热量$Q_{水}=Q_0×10$。
根据热量公式$Q = cm\Delta t$(其中$Q$为吸收的热量,$c$为比热容,$m$为质量,$\Delta t$为温度变化量),冰的质量$m_{冰}=m_{水}=50g = 0.05kg$,冰的温度变化量$\Delta t_{冰}=0^{\circ}C - (-10^{\circ}C)=10^{\circ}C$,水的温度变化量$\Delta t_{水}=10^{\circ}C - 0^{\circ}C = 10^{\circ}C$。
对于冰有$Q_{冰}=c_{冰}m_{冰}\Delta t_{冰}$,即$Q_0×5 = c_{冰}×0.05kg×10^{\circ}C$ ①;对于水有$Q_{水}=c_{水}m_{水}\Delta t_{水}$,即$Q_0×10 = c_{水}×0.05kg×10^{\circ}C$ ②。
用①$÷$②可得:$\frac{Q_0×5}{Q_0×10}=\frac{c_{冰}×0.05kg×10^{\circ}C}{c_{水}×0.05kg×10^{\circ}C}$,化简得$\frac{c_{冰}}{c_{水}}=\frac{1}{2}$。
2. 求冰在熔化过程中吸收的热量:
由图像可知,冰熔化过程用时$15min - 5min = 10min$,水从$0^{\circ}C$升高到$10^{\circ}C$用时$10min$。
水吸收的热量$Q_{水吸}=c_{水}m_{水}\Delta t_{水}=4.2×10^{3}J/(kg\cdot^{\circ}C)×0.05kg×(10^{\circ}C - 0^{\circ}C)=2.1×10^{3}J$。
因为单位时间内吸收的热量相同,且冰熔化时间与水升温时间相同,所以冰在熔化过程中吸收的热量$Q_{熔化}=Q_{水吸}=2.1×10^{3}J$。
【答案】:$1:2$;$2.1×10^3$
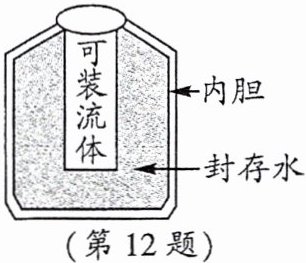
12. *网上曾热销一种“55度杯”,称“能很快将开水变成适饮的温水,而后又能将凉水变成适饮的温水”。为破解此中秘密,某中学物理小组设计了如图所示的模型。设此模型杯内胆中封存着300g水,室温为20℃;现向杯中倒入200g、100℃的开水,摇一摇,热平衡后杯内水温迅速降至$t_1= $
52
℃;然后将杯内水倒掉,迅速将200g室温某液体倒入该杯中,摇一摇,热平衡后这种液体的温度升至44℃,则这种液体的比热容为$2.1×10^3$
J/(kg·℃)。[c水$= 4.2×10^3J/(kg·℃),$忽略整个过程中内胆及空间的热损失]
答案:
【解析】:本题可根据热平衡方程$Q_{吸}=Q_{放}$来分别计算热平衡后的水温以及液体的比热容。
步骤一:计算倒入开水后热平衡时杯内水温$t_1$
已知向杯中倒入$m_{开水}=200g = 0.2kg$、$100^{\circ}C$的开水,杯内胆中封存着$m_{水}=300g = 0.3kg$、室温$t_0 = 20^{\circ}C$的水。
设热平衡后杯内水温为$t_1$,根据热平衡方程$Q_{吸}=Q_{放}$,即热水放出的热量等于冷水吸收的热量。
热水放出的热量$Q_{放}=c_{水}m_{开水}(100^{\circ}C - t_1)$,冷水吸收的热量$Q_{吸}=c_{水}m_{水}(t_1 - 20^{\circ}C)$,则可得:
$c_{水}m_{开水}(100^{\circ}C - t_1)=c_{水}m_{水}(t_1 - 20^{\circ}C)$
将$m_{开水}=0.2kg$,$m_{水}=0.3kg$代入上式,因为$c_{水}$不为$0$,两边同时约去$c_{水}$可得:
$0.2kg×(100^{\circ}C - t_1)=0.3kg×(t_1 - 20^{\circ}C)$
展开括号得:
$20 - 0.2t_1 = 0.3t_1 - 6$
移项可得:
$0.3t_1 + 0.2t_1 = 20 + 6$
合并同类项得:
$0.5t_1 = 26$
解得:
$t_1 = 52^{\circ}C$
步骤二:计算液体的比热容$c_{液}$
将杯内水倒掉后,迅速将$m_{液}=200g = 0.2kg$室温液体倒入该杯中,热平衡后这种液体的温度升至$44^{\circ}C$,此时杯内胆中原来水的温度为$52^{\circ}C$。
根据热平衡方程$Q_{吸}=Q_{放}$,液体吸收的热量$Q_{吸}=c_{液}m_{液}(44^{\circ}C - 20^{\circ}C)$,水放出的热量$Q_{放}=c_{水}m_{水}(52^{\circ}C - 44^{\circ}C)$,则可得:
$c_{液}m_{液}(44^{\circ}C - 20^{\circ}C)=c_{水}m_{水}(52^{\circ}C - 44^{\circ}C)$
将$m_{液}=0.2kg$,$m_{水}=0.3kg$,$c_{水}= 4.2×10^3J/(kg·℃)$代入上式可得:
$c_{液}×0.2kg×24^{\circ}C = 4.2×10^3J/(kg·℃)×0.3kg×8^{\circ}C$
$c_{液}×4.8 = 10080$
解得:
$c_{液}=2.1×10^3J/(kg·℃)$
【答案】:$52$;$2.1×10^3$
步骤一:计算倒入开水后热平衡时杯内水温$t_1$
已知向杯中倒入$m_{开水}=200g = 0.2kg$、$100^{\circ}C$的开水,杯内胆中封存着$m_{水}=300g = 0.3kg$、室温$t_0 = 20^{\circ}C$的水。
设热平衡后杯内水温为$t_1$,根据热平衡方程$Q_{吸}=Q_{放}$,即热水放出的热量等于冷水吸收的热量。
热水放出的热量$Q_{放}=c_{水}m_{开水}(100^{\circ}C - t_1)$,冷水吸收的热量$Q_{吸}=c_{水}m_{水}(t_1 - 20^{\circ}C)$,则可得:
$c_{水}m_{开水}(100^{\circ}C - t_1)=c_{水}m_{水}(t_1 - 20^{\circ}C)$
将$m_{开水}=0.2kg$,$m_{水}=0.3kg$代入上式,因为$c_{水}$不为$0$,两边同时约去$c_{水}$可得:
$0.2kg×(100^{\circ}C - t_1)=0.3kg×(t_1 - 20^{\circ}C)$
展开括号得:
$20 - 0.2t_1 = 0.3t_1 - 6$
移项可得:
$0.3t_1 + 0.2t_1 = 20 + 6$
合并同类项得:
$0.5t_1 = 26$
解得:
$t_1 = 52^{\circ}C$
步骤二:计算液体的比热容$c_{液}$
将杯内水倒掉后,迅速将$m_{液}=200g = 0.2kg$室温液体倒入该杯中,热平衡后这种液体的温度升至$44^{\circ}C$,此时杯内胆中原来水的温度为$52^{\circ}C$。
根据热平衡方程$Q_{吸}=Q_{放}$,液体吸收的热量$Q_{吸}=c_{液}m_{液}(44^{\circ}C - 20^{\circ}C)$,水放出的热量$Q_{放}=c_{水}m_{水}(52^{\circ}C - 44^{\circ}C)$,则可得:
$c_{液}m_{液}(44^{\circ}C - 20^{\circ}C)=c_{水}m_{水}(52^{\circ}C - 44^{\circ}C)$
将$m_{液}=0.2kg$,$m_{水}=0.3kg$,$c_{水}= 4.2×10^3J/(kg·℃)$代入上式可得:
$c_{液}×0.2kg×24^{\circ}C = 4.2×10^3J/(kg·℃)×0.3kg×8^{\circ}C$
$c_{液}×4.8 = 10080$
解得:
$c_{液}=2.1×10^3J/(kg·℃)$
【答案】:$52$;$2.1×10^3$
13. *物理兴趣小组的同学在研究“沙子和水谁的吸热本领大”实验时,选用了两只完全相同的酒精灯分别给质量都是200g的沙子和水加热,他们绘制出沙子与水的温度随加热时间变化的图像如图所示。已知水的比热容是$4.2×10^3J/(kg·℃),$请问:

(1)
(2)加热满2min时,水吸收了多少热量?
(3)试求出沙子的比热容。

(1)
a
由于沙子的比热容小,质量相同,吸热相同时,升温更快,所以沙子吸热升温是图像中的______图。(2)加热满2min时,水吸收了多少热量?
(3)试求出沙子的比热容。
答案:
(1)a
(2)解:由图b可知,加热2min时水的温度从20℃升高到70℃,水的质量$m_水=200g=0.2kg$,温度变化$\Delta t_水=70℃ - 20℃ = 50℃$。
根据热量计算公式$Q_吸 = c_水m_水\Delta t_水$,可得水吸收的热量:
$Q_吸 = 4.2×10^3J/(kg·℃)×0.2kg×50℃ = 4.2×10^4J$
(3)解:相同的酒精灯加热相同时间,沙子和水吸收的热量相同,即$Q_沙吸 = Q_水吸 = 4.2×10^4J$。
由图a可知,加热2min时沙子的温度从20℃升高到250℃,沙子的质量$m_沙=200g=0.2kg$,温度变化$\Delta t_沙=250℃ - 20℃ = 230℃$。
根据$Q_吸 = cm\Delta t$,可得沙子的比热容$c_沙=\frac{Q_沙吸}{m_沙\Delta t_沙}=\frac{4.2×10^4J}{0.2kg×230℃}\approx0.91×10^3J/(kg·℃)$
(1)a
(2)解:由图b可知,加热2min时水的温度从20℃升高到70℃,水的质量$m_水=200g=0.2kg$,温度变化$\Delta t_水=70℃ - 20℃ = 50℃$。
根据热量计算公式$Q_吸 = c_水m_水\Delta t_水$,可得水吸收的热量:
$Q_吸 = 4.2×10^3J/(kg·℃)×0.2kg×50℃ = 4.2×10^4J$
(3)解:相同的酒精灯加热相同时间,沙子和水吸收的热量相同,即$Q_沙吸 = Q_水吸 = 4.2×10^4J$。
由图a可知,加热2min时沙子的温度从20℃升高到250℃,沙子的质量$m_沙=200g=0.2kg$,温度变化$\Delta t_沙=250℃ - 20℃ = 230℃$。
根据$Q_吸 = cm\Delta t$,可得沙子的比热容$c_沙=\frac{Q_沙吸}{m_沙\Delta t_沙}=\frac{4.2×10^4J}{0.2kg×230℃}\approx0.91×10^3J/(kg·℃)$
查看更多完整答案,请扫码查看


