第132页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
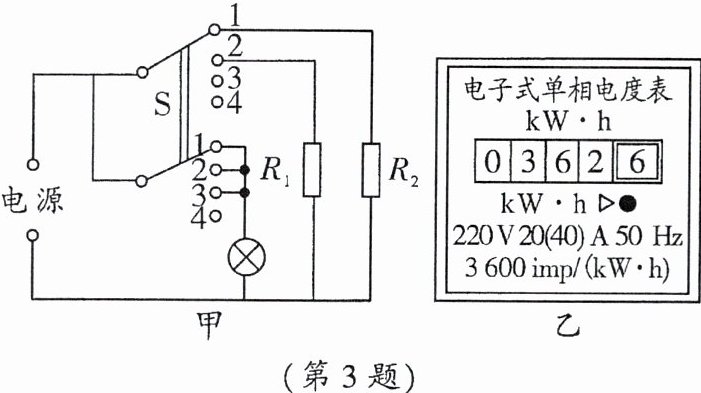
3.(2025·八中)如图甲所示是小高家的新型浴霸灯的原理图,它有“强热”“温热”“仅照明”及“停”四挡。图中S为“双刀四掷”开关,“双刀”在拨动时可一起同时转向图中“1”“2”“3”或“4”中的某一位置,从而实现各挡位间的转换。$R_1$与$R_2$是电热丝$(R_1= 2R_2),$浴霸灯的部分参数如表所示。求:
|“强热”挡总功率|990 W|
|“温热”挡总功率| |
|“仅照明”挡总功率|22 W|
|额定电压|220 V|

(1)接在“仅照明”挡时,电路中的电流;
(2)接在“温热”挡时$R_1$的功率;
(3)某天用电高峰期时,小高想利用家中电能表(如图乙)来测量家庭电路的实际电压,他断开家里的其他用电器,仅将浴霸灯调到“强热”挡上工作110 s,电能表的表盘闪烁了90次,求小高家里此时的实际电压。
|“强热”挡总功率|990 W|
|“温热”挡总功率| |
|“仅照明”挡总功率|22 W|
|额定电压|220 V|

(1)接在“仅照明”挡时,电路中的电流;
(2)接在“温热”挡时$R_1$的功率;
(3)某天用电高峰期时,小高想利用家中电能表(如图乙)来测量家庭电路的实际电压,他断开家里的其他用电器,仅将浴霸灯调到“强热”挡上工作110 s,电能表的表盘闪烁了90次,求小高家里此时的实际电压。

答案:
解:
(1)接在“仅照明”挡时,由$P = UI$得,电路中的电流:$I=\frac{P_{照明}}{U}=\frac{22W}{220V}=0.1A$。
(2)设$R_{2}=R$,则$R_{1}=2R$。“强热”挡功率最大,两电阻并联,总功率$P_{强热}=\frac{U^{2}}{R_{1}}+\frac{U^{2}}{R_{2}}=\frac{(220V)^{2}}{2R}+\frac{(220V)^{2}}{R}=990W$,解得$R = 40\Omega$,则$R_{1}=80\Omega$,$R_{2}=40\Omega$。“温热”挡为单个电阻工作,功率较小的为$R_{1}$,$P_{1}=\frac{U^{2}}{R_{1}}=\frac{(220V)^{2}}{80\Omega}=605W$。
(3)电能表参数$3600imp/(kW\cdot h)$,闪烁90次消耗电能$W=\frac{90}{3600}kW\cdot h = 0.025kW\cdot h=9×10^{4}J$。实际功率$P_{实}=\frac{W}{t}=\frac{9×10^{4}J}{110s}=\frac{9000}{11}W$。“强热”挡总电阻$R_{总}=\frac{R_{1}R_{2}}{R_{1}+R_{2}}=\frac{80\Omega×40\Omega}{80\Omega + 40\Omega}=\frac{80}{3}\Omega$。由$P_{实}=\frac{U_{实}^{2}}{R_{总}}$得$U_{实}=\sqrt{P_{实}R_{总}}=\sqrt{\frac{9000}{11}W×\frac{80}{3}\Omega}=200V$。
答案:
(1)0.1A;
(2)605W;
(3)200V。
(1)接在“仅照明”挡时,由$P = UI$得,电路中的电流:$I=\frac{P_{照明}}{U}=\frac{22W}{220V}=0.1A$。
(2)设$R_{2}=R$,则$R_{1}=2R$。“强热”挡功率最大,两电阻并联,总功率$P_{强热}=\frac{U^{2}}{R_{1}}+\frac{U^{2}}{R_{2}}=\frac{(220V)^{2}}{2R}+\frac{(220V)^{2}}{R}=990W$,解得$R = 40\Omega$,则$R_{1}=80\Omega$,$R_{2}=40\Omega$。“温热”挡为单个电阻工作,功率较小的为$R_{1}$,$P_{1}=\frac{U^{2}}{R_{1}}=\frac{(220V)^{2}}{80\Omega}=605W$。
(3)电能表参数$3600imp/(kW\cdot h)$,闪烁90次消耗电能$W=\frac{90}{3600}kW\cdot h = 0.025kW\cdot h=9×10^{4}J$。实际功率$P_{实}=\frac{W}{t}=\frac{9×10^{4}J}{110s}=\frac{9000}{11}W$。“强热”挡总电阻$R_{总}=\frac{R_{1}R_{2}}{R_{1}+R_{2}}=\frac{80\Omega×40\Omega}{80\Omega + 40\Omega}=\frac{80}{3}\Omega$。由$P_{实}=\frac{U_{实}^{2}}{R_{总}}$得$U_{实}=\sqrt{P_{实}R_{总}}=\sqrt{\frac{9000}{11}W×\frac{80}{3}\Omega}=200V$。
答案:
(1)0.1A;
(2)605W;
(3)200V。
查看更多完整答案,请扫码查看


