《2025年高分突破课时达标讲练测九年级物理全一册沪科版》

6. 智能手机在出厂前,要对屏幕进行抗撞击试验。利用如图甲所示的传感电路进行测试。在测试时,将手机样品(不计质量)平放在压力传感器上,闭合开关S,自由释放重物,撞击后手机样品屏幕仍完好无损。从重物开始下落到撞击样品的过程中,记录了电流表的示数I随时间t变化的图像如图乙所示,压力传感器的电阻R随压力F变化规律的图像如图丙所示。已知电源电压为22 V,定值电阻$R_{0}= 10\ \Omega$。下列说法正确的是(D)

A.压力越大,压力传感器的电阻越大
B.压力越大,定值电阻$R_{0}$两端电压变小
C.重物落到手机样品屏幕前,压力传感器的电阻为110 Ω
D.当压力增大到600 N时,此时电路中的电流是1.1 A

答案： D

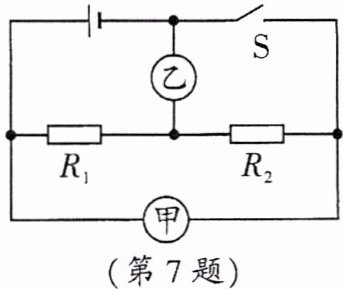
7. (2024·凉山州)如图所示的电路中$R_{1}:R_{2}= 1:2$,当开关S闭合,甲、乙两表均为电压表时,两电压表示数之比为3:2;当开关S断开,甲、乙两表均为电流表时,两电流表示数之比为1:3。

答案： 解：情况一：开关S闭合，甲、乙为电压表
电路中$R_1$、$R_2$串联，甲测电源电压$U$，乙测$R_2$电压$U_2$
设$R_1=R$，则$R_2=2R$，电流$I=\frac{U}{R+2R}=\frac{U}{3R}$
$U_2=I R_2=\frac{U}{3R}×2R=\frac{2U}{3}$
$\frac{U_甲}{U_乙}=\frac{U}{\frac{2U}{3}}=\frac{3}{2}$
情况二：开关S断开，甲、乙为电流表
电路中$R_1$、$R_2$并联，甲测$R_2$电流$I_2$，乙测干路电流$I$
电源电压$U$，$I_1=\frac{U}{R}$，$I_2=\frac{U}{2R}$，$I=I_1+I_2=\frac{U}{R}+\frac{U}{2R}=\frac{3U}{2R}$
$\frac{I_甲}{I_乙}=\frac{I_2}{I}=\frac{\frac{U}{2R}}{\frac{3U}{2R}}=\frac{1}{3}$
答案：$3:2$；$1:3$

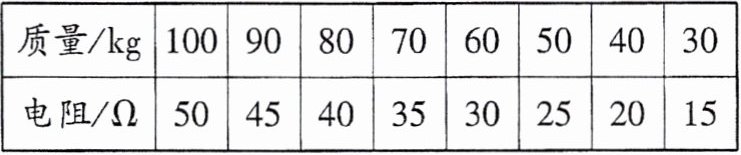
8. (2025·育才)小明购买了一个可以设定健康提示的电子体重秤,如图甲所示,当所测质量大于等于80 kg时蜂鸣器发出提示音。小明通过查询资料了解电子体重秤,电子秤简化电路图如图乙所示(蜂鸣器未画出)。已知电源电压为6 V,电压表示数大于等于3 V时蜂鸣器启动,$R_{0}$为保护电路的定值电阻,$R_{x}$为压敏电阻,压敏电阻大小与质量的关系如表所示。求:
(1)$R_{0}$的阻值为多少?
(2)当测得体重为70 kg时,电压表的示数为多少?
(3)通过查阅资料得知,身高1.70 m的小明,标准体重为60 kg。请在原来电路的基础上进行改进,将体重秤设置为大于等于60 kg时蜂鸣器发出提示音,并通过计算说明可行性。
|质量/kg|100|90|80|70|60|50|40|30|
|电阻/Ω|50|45|40|35|30|25|20|15|

答案： 【解析】：
本题主要考查串联电路的特点、欧姆定律以及电路的动态分析。
（1）由电路图可知，$R_{0}$与$R_{x}$串联，电压表测$R_{x}$两端的电压。当所测质量大于等于$80kg$时，蜂鸣器发出提示音，此时电压表示数大于等于$3V$，由表格数据可知，当质量为$80kg$时，压敏电阻$R_{x}=40\Omega$，此时电路中的电流$I = \frac{U_{x}}{R_{x}}=\frac{3V}{40\Omega}=0.075A$，$R_{0}$两端的电压$U_{0}=U - U_{x}=6V - 3V = 3V$，则$R_{0}$的阻值$R_{0}=\frac{U_{0}}{I}=\frac{3V}{0.075A}=40\Omega$。
（2）由表格数据可知，当测得体重为$70kg$时，压敏电阻$R_{x}' = 35\Omega$，此时电路中的电流$I'=\frac{U}{R_{0}+R_{x}'}=\frac{6V}{40\Omega + 35\Omega}=0.08A$，电压表的示数$U_{x}' = I'R_{x}' = 0.08A×35\Omega = 2.8V$。
（3）当质量为$60kg$时，压敏电阻$R_{x}'' = 30\Omega$，此时电路中的电流$I''=\frac{U}{R_{0}+R_{x}''}=\frac{6V}{40\Omega + 30\Omega}=\frac{3}{35}A$，$R_{x}$两端的电压$U_{x}'' = I''R_{x}''=\frac{3}{35}A×30\Omega\approx2.57V\lt 3V$，所以可以通过减小$R_{0}$的阻值来实现当体重达到$60kg$时蜂鸣器发出提示音。
【答案】：
(1)解：由电路图可知，$R_{0}$与$R_{x}$串联，电压表测$R_{x}$两端的电压。当所测质量大于等于$80kg$时，蜂鸣器发出提示音，此时电压表示数大于等于$3V$，由表格数据可知，当质量为$80kg$时，压敏电阻$R_{x}=40\Omega$，此时电路中的电流$I = \frac{U_{x}}{R_{x}}=\frac{3V}{40\Omega}=0.075A$，$R_{0}$两端的电压$U_{0}=U - U_{x}=6V - 3V = 3V$，则$R_{0}$的阻值$R_{0}=\frac{U_{0}}{I}=\frac{3V}{0.075A}=40\Omega$。
答：$R_{0}$的阻值为$40\Omega$。
(2)解：由表格数据可知，当测得体重为$70kg$时，压敏电阻$R_{x}' = 35\Omega$，此时电路中的电流$I'=\frac{U}{R_{0}+R_{x}'}=\frac{6V}{40\Omega + 35\Omega}=0.08A$，电压表的示数$U_{x}' = I'R_{x}' = 0.08A×35\Omega = 2.8V$。
答：当测得体重为$70kg$时，电压表的示数为$2.8V$。
(3)解：当质量为$60kg$时，压敏电阻$R_{x}'' = 30\Omega$，此时电路中的电流$I''=\frac{U}{R_{0}+R_{x}''}=\frac{6V}{40\Omega + 30\Omega}=\frac{3}{35}A$，$R_{x}$两端的电压$U_{x}'' = I''R_{x}''=\frac{3}{35}A×30\Omega\approx2.57V\lt 3V$，所以可以通过减小$R_{0}$的阻值来实现当体重达到$60kg$时蜂鸣器发出提示音。
答：可以通过减小$R_{0}$的阻值来实现当体重达到$60kg$时蜂鸣器发出提示音。