19. 如图,在$\triangle ABC$中,$AB = AC$,点$D$,$E$,$F分别在边AB$,$BC$,$AC$上,且$BE = CF$,$BD = CE$。
(1) 求证:$\triangle DEF$是等腰三角形;
(2) 当$\angle A = 40^{\circ}$时,求$\angle DEF$的度数。
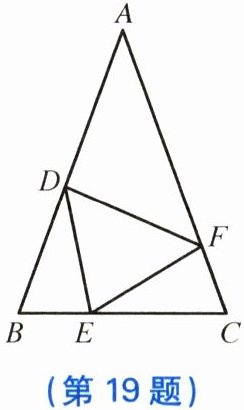
(1) 求证:$\triangle DEF$是等腰三角形;
(2) 当$\angle A = 40^{\circ}$时,求$\angle DEF$的度数。

答案:
(1)
∵AB=AC,
∴∠B=∠C.在△DBE和△ECF中,{BE=CF,∠B=∠C,BD=CE},
∴△DBE≌△ECF.
∴DE=EF.
∴△DEF是等腰三角形
(2)由
(1)可知△DBE≌△ECF.
∴∠BDE=∠CEF.
∵∠A+∠B+∠C=180°,∠A=40°,∠B=∠C,
∴∠B=70°.
∴∠BDE+∠DEB=110°.
∴∠CEF+∠DEB=110°.
∴∠DEF=70°
(1)
∵AB=AC,
∴∠B=∠C.在△DBE和△ECF中,{BE=CF,∠B=∠C,BD=CE},
∴△DBE≌△ECF.
∴DE=EF.
∴△DEF是等腰三角形
(2)由
(1)可知△DBE≌△ECF.
∴∠BDE=∠CEF.
∵∠A+∠B+∠C=180°,∠A=40°,∠B=∠C,
∴∠B=70°.
∴∠BDE+∠DEB=110°.
∴∠CEF+∠DEB=110°.
∴∠DEF=70°
20. 如图,$\triangle ABC和\triangle ADE$都是等腰直角三角形,$\angle BAC = \angle DAE = 90^{\circ}$,$CE与BD相交于点O$,$BD交AC于点G$。求证:
(1) $BD = CE$;
(2) $BD \perp CE$。
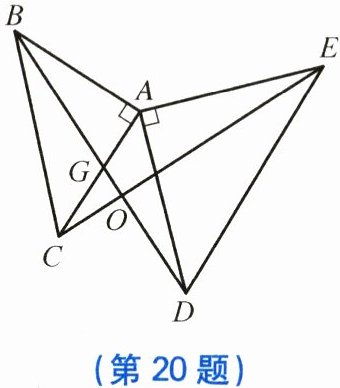
(1) $BD = CE$;
(2) $BD \perp CE$。

答案:
(1)
∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°.
∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE.
∴△ABD≌△ACE.
∴BD=CE
(2)
∵△ABD≌△ACE,
∴∠ABD=∠ACE.
∵∠BGA=∠CGO,
∴∠COG=∠BAG=90°,即BD⊥CE
(1)
∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°.
∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE.
∴△ABD≌△ACE.
∴BD=CE
(2)
∵△ABD≌△ACE,
∴∠ABD=∠ACE.
∵∠BGA=∠CGO,
∴∠COG=∠BAG=90°,即BD⊥CE
查看更多完整答案,请扫码查看


