《2025年同步练习上海科学技术出版社八年级数学上册沪科版》

17. 如图,在四边形$ABCD$中,$DC // AB$,$\angle 1 + \angle A = 90^{\circ}$,求证：$AD \perp DB$。

答案：
∵DC//AB,
∴∠1+∠ADB+∠A=180°.
∵∠1+∠A=90°,
∴∠ADB=90°,即AD⊥DB

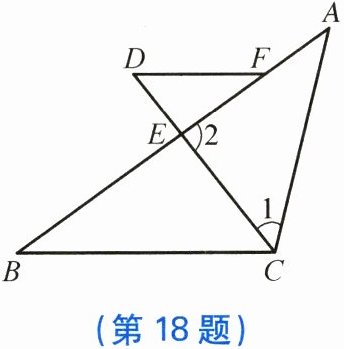
18. 如图,在$\triangle ABC$中,$CD平分\angle ACB交边AB于点E$,在$AE上取点F$,连接$DF$,使$\angle 1 = \angle D$。
(1)求证：$DF // BC$；
(2)当$\angle A = 36^{\circ}$,$\angle DFE = 34^{\circ}$时,求$\angle 2$的度数。

答案：
(1)
∵CD平分∠ACB,
∴∠DCB=∠1.
∵∠1=∠D,
∴∠DCB=∠D.
∴DF//BC
(2)
∵DF//BC,∠DFE=34°,
∴∠B=∠DFE=34°.
∵在△ABC中,∠A=36°,∠B=34°,
∴∠ACB=110°.
∵CD平分∠ACB,
∴∠1= $\frac{1}{2}$∠ACB=55°.
∴∠2=89°