19. 在平面直角坐标系中,已知点 $ A $,$ B $,$ C $ 的坐标分别为 $ A(-2,1) $,$ B(3,1) $,$ C(2,3) $。请回答下列问题:
(1) 在图中描出点 $ A $,$ B $,$ C $;
(2) 求 $ \triangle ABC $ 的面积;
(3) 在 $ y $ 轴上是否存在点 $ P $,使 $ \triangle ABP $ 的面积为 $ 10 $。若存在,请直接写出点 $ P $ 的坐标;若不存在,请说明理由。

(1) 在图中描出点 $ A $,$ B $,$ C $;
(2) 求 $ \triangle ABC $ 的面积;
(3) 在 $ y $ 轴上是否存在点 $ P $,使 $ \triangle ABP $ 的面积为 $ 10 $。若存在,请直接写出点 $ P $ 的坐标;若不存在,请说明理由。

答案:
(1)略
(2)5
(3)存在.点P的坐标为$(0,5)$或$(0,-3)$
(1)略
(2)5
(3)存在.点P的坐标为$(0,5)$或$(0,-3)$
20. 如图,在平面直角坐标系中,$ A $,$ B $,$ C $ 三点的坐标分别为 $ A(0,1) $,$ B(2,0) $,$ C\left(2,\dfrac{3}{2}\right) $。
(1) 求 $ \triangle ABC $ 的面积;
(2) 如果在第二象限内有一点 $ P(a,\sqrt{2}) $,试用含 $ a $ 的式子表示四边形 $ ABOP $ 的面积;
(3) 在(2)的条件下,是否存在点 $ P $,使得四边形 $ ABOP $ 的面积与 $ \triangle ABC $ 的面积相等?若存在,请求出点 $ P $ 的坐标;若不存在,请说明理由。
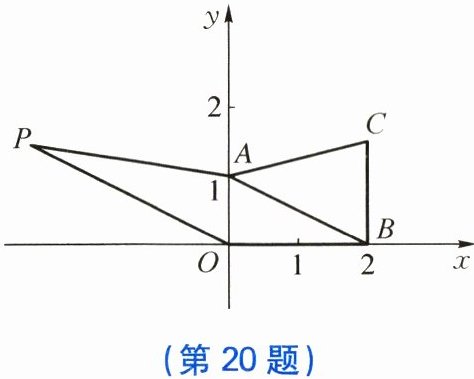
(1) 求 $ \triangle ABC $ 的面积;
(2) 如果在第二象限内有一点 $ P(a,\sqrt{2}) $,试用含 $ a $ 的式子表示四边形 $ ABOP $ 的面积;
(3) 在(2)的条件下,是否存在点 $ P $,使得四边形 $ ABOP $ 的面积与 $ \triangle ABC $ 的面积相等?若存在,请求出点 $ P $ 的坐标;若不存在,请说明理由。

答案:
(1)$\frac{3}{2}$
(2)$1-\frac{1}{2}a$
(3)存在,点P的坐标为$(-1,\sqrt{2})$
(1)$\frac{3}{2}$
(2)$1-\frac{1}{2}a$
(3)存在,点P的坐标为$(-1,\sqrt{2})$
查看更多完整答案,请扫码查看


