14. 如图,在$\triangle ABC$中,$AD$是边 $BC$上的中线,$BE是\triangle ABD$的中线。若$\triangle ABC$的面积是 $24$,$AE = 6$,则点 $B$到 $ED$的距离是______.


答案:
2
15. 在$\triangle ABC$中,$\angle A = 50^{\circ}$,$\angle B = 30^{\circ}$,点 $D$在边 $AB$上,连接 $CD$。若$\triangle ACD$为直角三角形,则$\angle BCD$的度数为______.
答案:
60°或10°
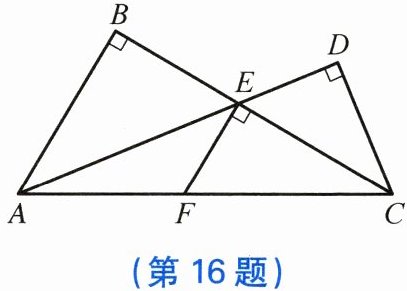
16. 在$\triangle ABC和\triangle ADC$中,$\angle B= \angle D = 90^{\circ}$,$AD$,$BC$交于点 $E$,$EF\perp BC$交 $AC$于点 $F$。
(1) 在$\triangle ABC$中,边 $BC$上的高是______;
(2) 在$\triangle AEC$中,边 $AE$上的高是______;
(3) 若 $AB = 8$,$AE = 10$,$CD = 6$,求$\triangle AEC$的面积及 $CE$的长。
(1) 在$\triangle ABC$中,边 $BC$上的高是______;
(2) 在$\triangle AEC$中,边 $AE$上的高是______;
(3) 若 $AB = 8$,$AE = 10$,$CD = 6$,求$\triangle AEC$的面积及 $CE$的长。

答案:
(1) AB
(2) CD
(3) $S_{\triangle AEC}=\frac{1}{2}AE\cdot CD=\frac{1}{2}×10×6=30$. 由$\frac{1}{2}CE\cdot AB=30$可得$CE=7.5$
(1) AB
(2) CD
(3) $S_{\triangle AEC}=\frac{1}{2}AE\cdot CD=\frac{1}{2}×10×6=30$. 由$\frac{1}{2}CE\cdot AB=30$可得$CE=7.5$
查看更多完整答案,请扫码查看


