《2025年同步练习上海科学技术出版社八年级数学上册沪科版》

21. 在△ABC中,∠ACB= 90°,AC= BC,直线MN过点C,且AD⊥MN于点D,BE⊥MN于点E.
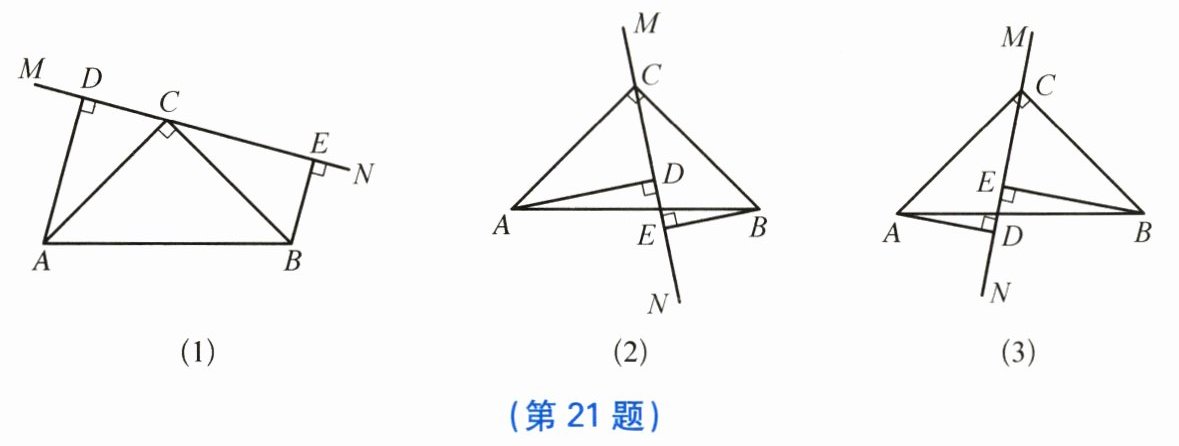
(1) 当直线MN绕点C旋转到图(1)的位置时,求证：DE= AD+BE；
(2) 当直线MN绕点C旋转到图(2)的位置时,求证：DE= AD-BE；
(3) 当直线MN绕点C旋转到图(3)的位置时,DE,AD,BE有怎样的等量关系? 请写出这个等量关系,并加以证明.

答案：
(1) 提示：证明 $\triangle ACD \cong \triangle CBE$，则 $DC=EB$，$CE=AD$.$\therefore DE=AD+BE$
(2) 提示：证法同
(1)
(3) $DE=BE-AD$.提示：证法同
(1)