《2025年同步练习上海科学技术出版社八年级数学上册沪科版》

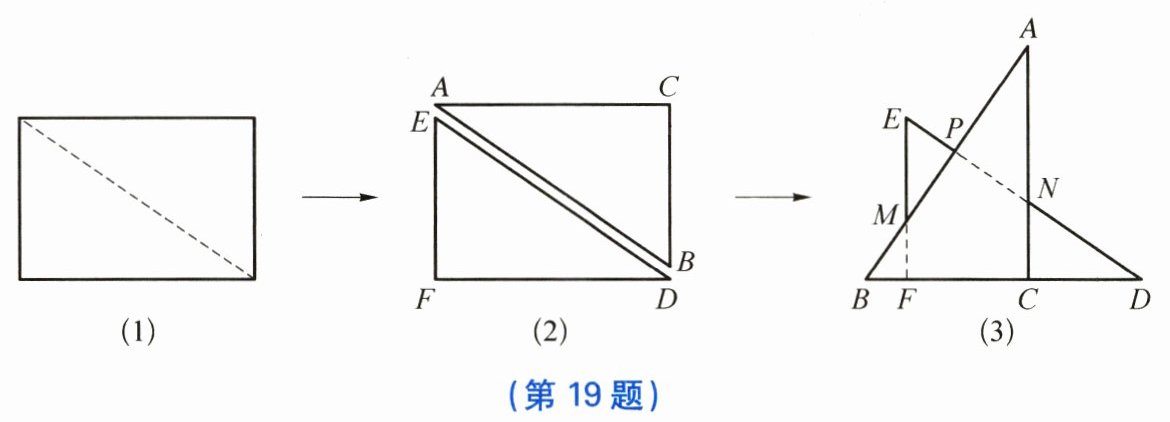
19. 如图(1),(2),一张长方形纸片沿对角线剪开,得到两张三角形纸片,再将这两张三角形纸片按图(3)所示摆放,使点B,F,C,D在同一条直线上.
(1) 如图(3),求证：AB⊥ED；
(2) 如图(3),若PB= BC,请找出图中一对全等三角形(△ABC≌△DEF除外),并给予证明.

答案：
(1) 提示：由 $\triangle ABC \cong \triangle DEF$，得 $\angle A= \angle D$，从而可证明 $\angle APD=90°$
(2) 答案不唯一.如：$\triangle DBP \cong \triangle ABC$，证明略

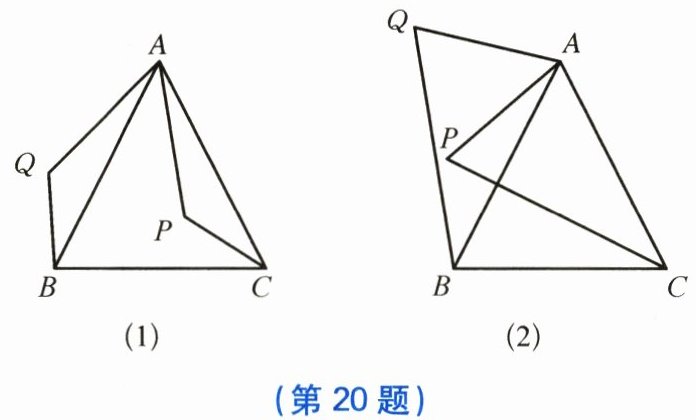
20. 复习“全等三角形”的知识时,老师布置了一道作业题：“如图(1),在△ABC中,AB= AC,P是△ABC内任意一点,将AP绕点A顺时针旋转至AQ,使∠QAP= ∠BAC.连接BQ,CP,则BQ= CP.”
小亮是个爱动脑筋的同学,他通过对图(1)的分析,证明了△ABQ≌△ACP,从而证得BQ= CP.之后,他将点P移到△ABC之外,原题中其他条件不变,发现“BQ= CP”仍然成立,请你根据图(2)给出证明.

答案： 提示：证明 $\triangle ABQ \cong \triangle ACP$