《2025年初中必刷题七年级数学上册苏科版》

1[2024原创]下列说法中,正确的是(B)
A.角的两边画得越长,这个角就越大
B.角的大小与它的两边张开的程度有关
C.若$∠A+∠B＞∠C$,那么$∠A一定大于∠C$
D.放大镜可以把角的度数放大

答案： B　[解析]角的大小与它的两边张开的程度有关，与角的两边的长短无关，所以A、D选项错误，B选项正确；若∠A+∠B＞∠C，那么∠A 与∠C的大小关系无法确定，所以C选项错误.故选B.

2新考法[2025福建宁德期末]比较两个角的大小关系:小明用度量法测得$∠AOB= 45^{\circ },$$∠COD= 50^{\circ }$;小丽用叠合法比较,将$∠AOB和∠COD$的顶点重合,边OB与OD重合,边OA和OC置于重合边的同侧,则边OA____.(填序号:①在$∠COD$的内部;②在$∠COD$的外部;③与边OC重合)

答案：
①　[解析]因为∠AOB=45°，∠COD=50°，所以∠AOB＜∠COD，所以用叠合法比较如图所示，OA在∠COD的内部.故答案为①.

3[2024浙江台州期中]如图,根据$∠α利用尺规作图作∠AOB$,若$∠AOB= 70^{\circ }$,可知$∠α$的度数为35°.

答案： 35°　[解析]由尺规作图的痕迹可知∠AOB=2∠α，所以2∠α=70°，所以∠α=35°.故答案为35°.

4[2025陕西西安期末]如图,已知$∠α,∠AOB= $$90^{\circ }$,求作$∠AOC$,使其等于$∠α$的余角.(保留作图痕迹,不写作法)

答案：
[解]如图所示，∠AOC就是所求作的角.

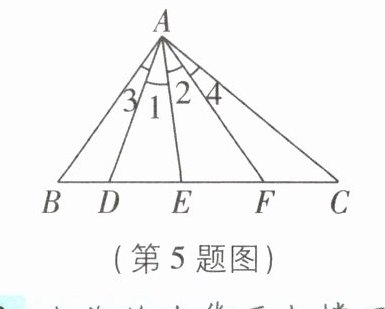
5如图,$∠1= ∠2,∠3= ∠4$,则下列结论正确的有(C)
①AD平分$∠BAE$;②AF平分$∠EAC$;③AE平分$∠DAF$;④AF平分$∠BAC$;⑤AE平分$∠BAC$.

A.4个
B.3个
C.2个
D.1个

答案： C　[解析]因为∠1=∠2，所以AE平分∠DAF.因为∠1=∠2，∠3=∠4，所以∠BAE=∠CAE，所以AE平分∠BAC.所以正确的结论有2个.故选C.

6如图,OC是$∠AOB$的平分线,$∠AOB= 74^{\circ },$$∠COD= 10^{\circ }$,则$∠AOD$为(B)
A.$17^{\circ }$
B.$27^{\circ }$
C.$37^{\circ }$
D.$64^{\circ }$

答案： B　[解析]因为OC是∠AOB的平分线，∠AOB=74°，所以∠BOC=∠COA=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×74°=37°.因为∠AOC=∠COD+∠DOA，∠COD=10°，所以∠AOD=∠AOC−∠COD=37°−10°=27°.故选B.

7如图,一副直角三角板摆放在一起,且有一条边重合,射线OM平分$∠BOC$,ON平分$∠AOC,$$∠MON$的度数为45°.

答案： 45°　[解析]因为∠BOC=∠AOB+∠AOC=90°+30°=120°，射线OM平分∠BOC，所以∠COM=$\frac{1}{2}$∠BOC=$\frac{1}{2}$×120°=60°.因为ON平分∠AOC，所以∠CON=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×30°=15°，所以∠MON=∠COM−∠CON=60°−15°=45°.故答案为45°.

8点O在直线AD上,在直线AD的同侧作射线OB,OC.

(1)如图(1),若$∠AOB= 40^{\circ },∠BOC:∠COD= $$4:3$,求$∠BOC$的度数;
(2)如图(2),若OM平分$∠AOC$,ON平分$∠BOD,∠MON= 130^{\circ }$,求$∠BOC$的度数.

答案： [解]
(1)因为∠AOB=40°，所以∠BOD=180°−∠AOB=140°，所以∠BOC+∠COD=140°.因为∠BOC∶∠COD=4∶3，所以设∠BOC=4x，∠COD=3x，所以4x+3x=140°，所以x=20°，所以∠BOC=80°.
(2)因为∠MON=130°，所以∠AOM+∠DON=180°−∠MON=50°.因为OM平分∠AOC，ON平分∠BOD，所以∠AOM=∠COM，∠BON=∠DON，所以∠COM+∠BON=50°，所以∠BOC=∠MON−(∠COM+∠BON)=130°−50°=80°.
思路分析：
(1)先利用平角定义求出∠BOC+∠COD=140°，然后设∠BOC=4x，∠COD=3x，列出方程并求解，进而即可解答.
(2)先利用平角定义求出∠AOM+∠DON=50°，然后根据角平分线的定义求出∠COM+∠BON=50°，即可解答.
易错警示：当两个角共顶点且有公共边时，需要考虑一个角在另一个角内部和外部这两种情况，注意不要漏解.

9已知$∠AOB= 20^{\circ },∠AOC= 4∠AOB$,OD平分$∠AOB$,OM平分$∠AOC$,则$∠MOD$的度数是____.

答案：
30°或50°　[解析]因为∠AOB=20°，∠AOC=4∠AOB，所以∠AOC=80°.因为OD平分∠AOB，OM平分∠AOC，所以∠AOD=∠BOD=$\frac{1}{2}$∠AOB=10°，∠AOM=∠COM=$\frac{1}{2}$∠AOC=40°.分为两种情况：
①如图
(1)，当∠AOB在∠AOC的内部时，∠DOM=∠AOM−∠AOD=40°−10°=30°.
②如图
(2)，当∠AOB在∠AOC的外部时，∠DOM=∠AOM+∠AOD=40°+10°=50°.故答案为30°或50°.