《2025年初中必刷题七年级数学上册苏科版》

1[2024江苏徐州中考]观察下列各数：3,8,18,38,…,按此规律,第5~7个数可能为(D)
A.48,58,68
B.58,78,98
C.76,156,316
D.78,158,318

答案： D 【解析】因为3×2+2=8,8×2+2=18,18×2+2=38,所以第5个数为38×2+2=78,第6个数为78×2+2=158,第7个数为158×2+2=318,故选D.

2[2024江苏扬州中考]1202年数学家斐波那契在《计算之书》中记载了一列数：1,1,2,3,5,…,这一列数满足：从第三个数开始,每一个数都等于它的前两个数之和.则在这一列数的前2024个数中,奇数的个数为(D)
A.676
B.674
C.1348
D.1350

答案： D 【解析】观察这一列数:1,1,2,3,5,8,13,21,34,55,…,得到规律:从第一个数开始,每三个数为一组,每组数中前两个数是奇数,第三个数为偶数.因为2024=674×3+2,所以前2024个数分成674组,余2个数,所以这一列数的前2024个数中奇数有674×2+2=1350(个).故选D.

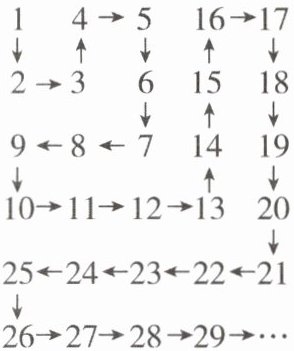
3[2024山东潍坊中考]将连续的正整数排成如图所示的数表.记$a_{(i,j)}$为数表中第i行第j列位置的数字,如$a_{(1,2)}= 4,a_{(3,2)}= 8,a_{(5,4)}= 22$.若$a_{(m,n)}= 2024$,则$m=$45,$n=$2.

答案： 45 2 【解析】由题图可知,当正整数为k²时,若k为奇数,则k²在第k行,第1列,k²+1在第(k+1)行,第1列,k²-1在第k行,第2列;若k为偶数,则k²在第1行,第k列,k²+1在第1行,第(k+1)列,k²-1在第2行,第k列.因为a(m,n)=2024=2025-1=45²-1,而2025=45²,在第45行,第1列,所以2024在第45行,第2列,所以m=45,n=2,故答案为45,2.

4[2023四川广元中考]在我国南宋数学家杨辉所著的《详解九章算术》(1261年)一书中,用如图的三角形解释二项和的乘方规律,因此我们称这个三角形为“杨辉三角”,根据规律第八行从左到右第三个数为21.

答案： 21 【解析】根据规律可得第七行的数字为1,6,15,20,15,6,1;第八行的数字为1,7,21,35,35,21,7,1,所以第八行从左到右第三个数为21,故答案为21.

5[2024山东济宁中考]如图,用大小相等的小正方形按照一定规律拼正方形.第一幅图有1个正方形,第二幅图有5个正方形,第三幅图有14个正方形……按照此规律,第六幅图中正方形的个数为(B)
A.90
B.91
C.92
D.93

答案： B 【解析】第一幅图中有1个正方形,第二幅图中有5=(1²+2²)个正方形,第三幅图中有14=(1²+2²+3²)个正方形,…,所以可推得第六幅图中有1²+2²+3²+4²+5²+6²=1+4+9+16+25+36=91(个)正方形,故选B.

6[2024青海中考]如图是由火柴棒摆成的图案,按此规律摆放,第(7)个图案中有15个火柴棒.

答案： 15 【解析】根据题意得题中第
(1)个图案中有3=(1+2)个火柴棒,第
(2)个图案中有5=(1+2×2)个火柴棒,第
(3)个图案中有7=(1+2×3)个火柴棒,…,第(n)个图案中有(1+2n)个火柴棒,所以第
(7)个图案中有1+2×7=15(个)火柴棒,故答案为15.

7[四川德阳中考]古希腊的毕达哥拉斯学派对整数进行了深入的研究,尤其注意形与数的关系,“多边形数”也称为“形数”,就是形与数的结合物.用点排成的图形如下：

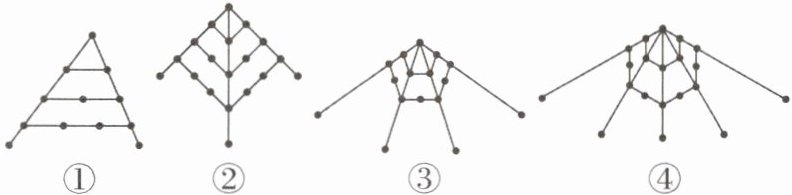
其中：图①的点数叫作三角形数,从上至下第一个三角形数是1,第二个三角形数是$1+2= 3$,第三个三角形数是$1+2+3= 6$,…；
图②的点数叫作正方形数,从上至下第一个正方形数是1,第二个正方形数是$1+3= 4$,第三个正方形数是$1+3+5= 9$,…；
……
由此类推,图④中第五个正六边形数是45.

答案： 45 【解析】题图①的点数叫作三角形数,从上至下第一个三角形数是1,第二个三角形数是1+2=3,第三个三角形数是1+2+3=6,…;题图②的点数叫作正方形数,从上至下第一个正方形数是1,第二个正方形数是1+3=4,第三个正方形数是1+3+5=9,…;题图③的点数叫作五边形数,从上至下第一个五边形数是1,第二个五边形数是1+4=5,第三个五边形数是1+4+7=12,…由此类推,题图④中第五个正六边形数是1+5+9+13+17=45.故答案为45.