《2025年拔尖特训数学五年级上册苏教版江苏专版》

8. 下面不同的图形代表不同的数字,相同的图形代表相同的数字。各图形分别代表多少？

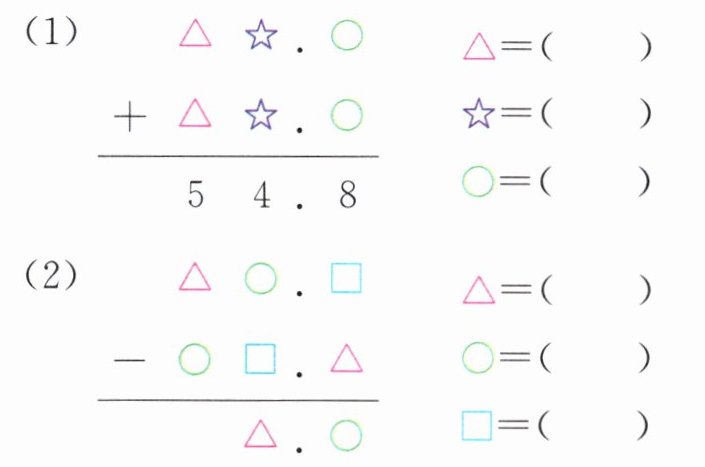
(1)△=2，☆=7，○=4
(2)△=5，○=4，□=9

答案：
(1)2 7 4 解析:两个△☆.◯相加的和的末位是 8,◯可能是 4 或 9,但个位上两个☆相加的和的末位是 4,是一个双数,说明十分位没有向个位进 1,所以十分位上的◯只能是 4,个位上的☆是 2 或 7。因为十位上的两个△相加的和是 5,是一个单数,说明个位向十位进了 1,所以☆是 7,△是 2。
(2)5 4 9 解析:先看十位,△ - ◯ = 0,说明△比◯大 1,且被个位借去了 1;再看个位,若十分位没有向个位借 1,则□ + 10 - ◯ = △,即□ + 10 - ◯ = ◯ + 1,此时□ = 9,十分位上□ - △ = ◯,即 9 - 5 = 4,所以△ = 5,◯ = 4。若十分位向个位借 1,则□ + 10 - 1 - ◯ = △,即□ + 9 - ◯ = △,此时□ = 8,十分位上 8 + 10 - △ = ◯。因为 18 不能分成两个相差 1 的数字,所以这种情况不成立。

9. 明明和花花各有一些零花钱,且明明比花花多 6.4 元。明明花去一半后,比花花少 1.8 元。明明和花花原来各有多少零花钱？

答案： 明明:6.4 + 1.8 = 8.2(元) 8.2 + 8.2 = 16.4(元) 花花:16.4 - 6.4 = 10(元) 解析:如图,明明原来比花花多 6.4 元,花去一半后,比花花少 1.8 元。由图可知,1.8 + 6.4 = 8.2(元)正好是明明花去的一半的零花钱,进而求出原来明明有多少零花钱,再减去明明比花花多的钱数得到花花原来有多少零花钱。

10. (数形结合)有一根绳子和一根竹竿,绳子比竹竿长 8.4 米,把绳子对折后比竹竿长 2.6 米。绳子和竹竿各长多少米？

答案： 绳子:8.4 - 2.6 = 5.8(米) 5.8 + 5.8 = 11.6(米) 竹竿:11.6 - 8.4 = 3.2(米) 解析:如图,绳子原来比竹竿长 8.4 米;对折后比竹竿长 2.6 米,即将绳子平均分成两份后,每份比竹竿长 2.6 米。由此可知,绳子一半的长度是 8.4 - 2.6 = 5.8(米),进而求出绳子原来的长度,再减去绳子原来比竹竿长的 8.4 米,即可得到竹竿的长度。

11. 桃桃用一根 28.5 米长的绳子做跳绳,第一次用去 8.5 米,做了 5 根短跳绳,第二次用去 12.32 米,做了 2 根长跳绳。这根绳子和原来比,短了多少米？

答案： 8.5 + 12.32 = 20.82(米) 解析:两次用去的绳子的长度之和,就是比原来短的长度。

12. *乐乐带着 50 元去超市,买了一袋鸡爪,用去 4.3 元,又买了一个文具盒,用去 10.8 元。乐乐现在身上的钱和原来比,少了多少元？

答案： 4.3 + 10.8 = 15.1(元) 解析:两次用去的钱数之和,就是比原来少的钱数。

13. (算法探究)计算：$1 - 0.99 - 0.98 + 0.97 + 0.96 - 0.95 - 0.94 + 0.93 + … + 0.04 - 0.03 - 0.02 + 0.01$。
思路提示：想一想,符号存在什么规律,可以怎样分组？

答案： 1 - 0.99 - 0.98 + 0.97 + 0.96 - 0.95 - 0.94 + 0.93 + … + 0.04 - 0.03 - 0.02 + 0.01 = (1 - 0.99 - 0.98 + 0.97) + (0.96 - 0.95 - 0.94 + 0.93) + … + (0.04 - 0.03 - 0.02 + 0.01) = 0 解析:每 4 个数分成一组,每组里两个加数的和正好等于两个减数的和,即每组的结果是 0。

14. 计算：$9.9 + 99.9 + 999.9 + 9999.9$。
思路提示：想一想,这些数分别接近哪个自然数？

答案： 9.9 + 99.9 + 999.9 + 9999.9 = 10 + 100 + 1000 + 10000 - 0.1 - 0.1 - 0.1 - 0.1 = 10 + 100 + 1000 + 10000 - 0.4 = 11110 - 0.4 = 11109.6 解析:可将算式中的这些数分别看作 10 - 0.1,100 - 0.1,1000 - 0.1,10000 - 0.1,则原算式变成 10 + 100 + 1000 + 10000 - 0.1 - 0.1 - 0.1 - 0.1。