《2025年拔尖特训数学五年级上册苏教版江苏专版》

1. (算法探究)如图,这个图形可以看作是由(长方)形与(梯)形组合而成的图形,也可以看作是由(长方)形剪掉一个(梯)形后得到的图形。

答案： 长方 梯 长方 梯

2. 计算下面图形的面积。

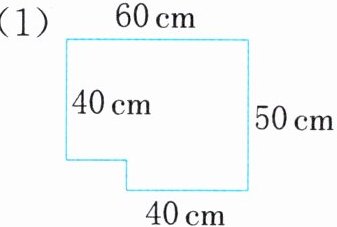
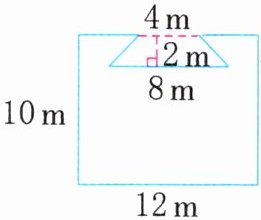
(2)

答案： （1）50×60-(50-40)×(60-40)=2800(cm²)
（2）12×10-(4+8)×2÷2=108(m²)
（3）35×18+35×10÷2=805(m²)
（4）5×6-(5-2)×(6-2)÷2=24(cm²)

3. 下面是一块空心地砖,朝上的一面是正方形(空心部分朝上的一面也是正方形)。它朝上的一面的实际面积是多少?

答案： 50×50-18×18=2176(cm²)

4. (泰州海陵区)如图所示为一家商场的大型广告牌示意图,每年要给这个广告牌的正反两面刷防锈漆,刷防锈漆的面积是多少平方米?

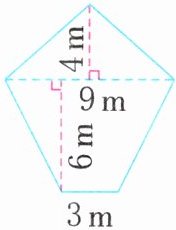
答案： (3+9)×6÷2+9×4÷2=54(m²)
54×2=108(m²)

5. 一块麦田(如图),今年共收小麦400吨,平均每公顷麦田可收小麦多少吨?

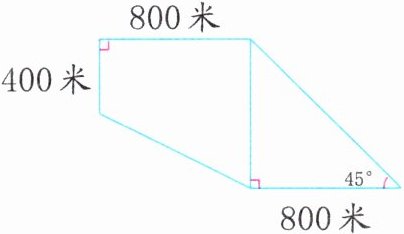
答案： (400+800)×800÷2=480000(平方米) 800×800÷2=320000(平方米) 480000+320000=800000(平方米) 800000平方米=80公顷 400÷80=5(吨) 解析：由题图可知，这块麦田由一个直角梯形和一个直角三角形组成，且易知该直角三角形的两条直角边相等，即这个直角三角形的两条直角边均是800米，梯形的下底是800米。据此可求出这块麦田的面积，从而求出平均每公顷麦田可收小麦多少吨。注意单位换算。

6. 如图,连接平行四边形四条边的中点,可得到一个新的平行四边形(涂色部分)。已知新的平行四边形的面积是24平方厘米,则原平行四边形的面积是多少平方厘米?

答案： 24×2=48(平方厘米) 解析：因为涂色部分是连接平行四边形四条边的中点得到的，所以涂色部分的面积等于空白部分的面积，即原平行四边形的面积是涂色部分面积的2倍。

7. (思维过程)公园里有一片三块正方形地相连的绿化带(如图),三块正方形地的边长分别是30米、20米、15米。绿化带中间有一个三角形花圃(涂色部分),这个三角形花圃的面积是多少平方米?

答案： 20×30÷2+20×(20+15)÷2=650(平方米)
解析：涂色部分的面积等于底为20米、高为30米的三角形与底为20米、高为(20+15)米的三角形的面积之和。