第17页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
(1) 在括号里填合适的数。
6 平方千米 = (
500 公顷 = (
30 平方千米 4 公顷 = (
6 平方千米 = (
6000000
) 平方米 = (600
) 公顷500 公顷 = (
5000000
) 平方米 = (5
) 平方千米30 平方千米 4 公顷 = (
3004
) 公顷
答案:
(1)6000000 600 5000000 5 3004
(1)6000000 600 5000000 5 3004
(2) 沙漏是古代一种计量时间的工具。如图所示为某个沙漏的截面示意图 (单位: cm), 则其截面的面积是 (
1344
) $\mathrm{cm}^2$。
答案:
(2)1344
(2)1344
2. 选一选。
(1) 如图, 先把一些练习本摞成一个长方体, 再把这摞练习本均匀地斜放, 比较从正面看到的两个图形, (
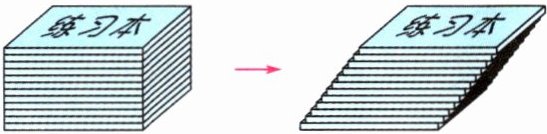
A.周长、面积都相等
B.周长、面积都不相等
C.周长不相等, 面积相等
D.周长相等, 面积不相等
(1) 如图, 先把一些练习本摞成一个长方体, 再把这摞练习本均匀地斜放, 比较从正面看到的两个图形, (
C
)。
A.周长、面积都相等
B.周长、面积都不相等
C.周长不相等, 面积相等
D.周长相等, 面积不相等
答案:
(1)C
(1)C
(2) 明明在估计右边树叶的面积时做了一些标记。若每个小方格表示 1 平方厘米, 则这片树叶的面积 (

A.大于 52 平方厘米
B.小于 22 平方厘米
C.等于 24 平方厘米
D.大约 37 平方厘米
D
)。
A.大于 52 平方厘米
B.小于 22 平方厘米
C.等于 24 平方厘米
D.大约 37 平方厘米
答案:
(2)D
(2)D
3. 计算下面图形的面积。(单位: 厘米)
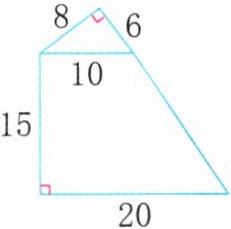

答案:
8×6÷2+(10+20)×15÷2=249(平方厘米)
4. 用宽度相等的铁皮做成一块字母标牌 (如图), 这块字母标牌的面积是多少平方分米?
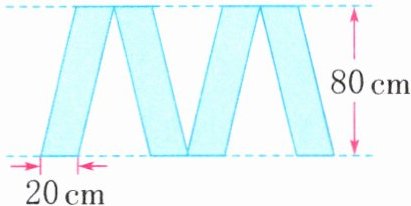

答案:
20cm=2dm 80cm=8dm
2×8×4=64(dm²)
2×8×4=64(dm²)
5. (生活应用) 若用木板制作这样的一块指示牌, 则至少需要多少平方厘米的木板?
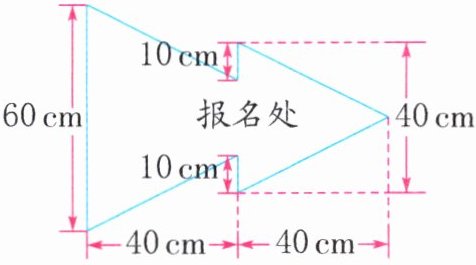

答案:
40×40÷2+(40−10×2+60)×40÷2=2400(cm²)
6. 如图, 在四边形 $A B C D$ 中, $\angle B= \angle D= 90^{\circ}$, $A B= 4$ 厘米, $C D= 6$ 厘米, $A E= 3$ 厘米, $F C= 5$ 厘米。涂色部分的面积是多少?
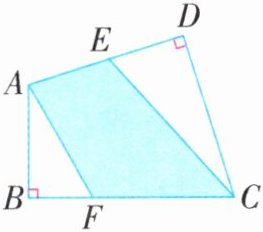

答案:
3×6÷2+5×4÷2=19(平方厘米)
解析:如图,连接AC。因为∠B=∠D=90°,所以CD是三角形AEC的高,AB是三角形AFC的高。由此分别求出三角形AEC和三角形AFC的面积并相加即可。

3×6÷2+5×4÷2=19(平方厘米)
解析:如图,连接AC。因为∠B=∠D=90°,所以CD是三角形AEC的高,AB是三角形AFC的高。由此分别求出三角形AEC和三角形AFC的面积并相加即可。

7. (思维过程) 如图, 在直角三角形 $A B C$ 中, $A B= 15$ 厘米, $B C= 10$ 厘米, 现在其内部画一个正方形 $D O E B$ 。正方形 $D O E B$ 的面积是多少平方厘米?
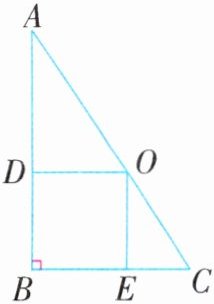
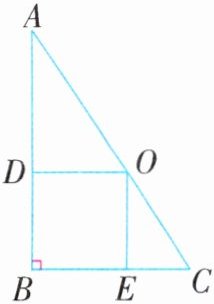
答案:
15×10÷2=75(平方厘米) 75×2÷(10+15)=6(厘米) 6×6=36(平方厘米)
解析:如图,连接OB,则三角形BOC的面积+三角形BOA的面积=三角形ABC的面积。因为四边形DOEB是正方形,所以DO=OE,即三角形BOC与三角形BOA的高相等。因此三角形BOA与三角形BOC的面积之和=AB×DO÷2+BC×OE÷2=(AB+BC)×DO÷2。又因为三角形ABC的面积=AB×BC÷2,所以(AB+BC)×DO÷2=AB×BC÷2。由此,可求出DO的长,即正方形DOEB的边长,从而求出其面积。

15×10÷2=75(平方厘米) 75×2÷(10+15)=6(厘米) 6×6=36(平方厘米)
解析:如图,连接OB,则三角形BOC的面积+三角形BOA的面积=三角形ABC的面积。因为四边形DOEB是正方形,所以DO=OE,即三角形BOC与三角形BOA的高相等。因此三角形BOA与三角形BOC的面积之和=AB×DO÷2+BC×OE÷2=(AB+BC)×DO÷2。又因为三角形ABC的面积=AB×BC÷2,所以(AB+BC)×DO÷2=AB×BC÷2。由此,可求出DO的长,即正方形DOEB的边长,从而求出其面积。

查看更多完整答案,请扫码查看


