2026年王朝霞考点梳理时习卷九年级数学全一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年王朝霞考点梳理时习卷九年级数学全一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 教材数学活动改编 如图,在同一时刻,身高1.6 m的小丽在阳光下的影长为2.5 m,一棵大树的影长为5 m,则这棵大树的高度为(

A.1.5 m
B.2.3 m
C.3.2 m
D.7.8 m
C
)
A.1.5 m
B.2.3 m
C.3.2 m
D.7.8 m
答案:
1.C
2.〔重庆市改编〕某小区门口的栏杆如图所示,栏杆从AC位置绕点O旋转到水平位置BD. 已知AB⊥BD,CD⊥BD,垂足分别为点B,D,AO = 4 m,AB = 1.6 m,CO = 1 m,则栏杆C端上升的垂直距离CD为(

A.0.2 m
B.0.3 m
C.0.4 m
D.0.5 m
C
)
A.0.2 m
B.0.3 m
C.0.4 m
D.0.5 m
答案:
2.C
3. 如图所示,某超市在一楼至二楼之间安装有电梯,天花板与地面平行. 张强扛着箱子(人与箱子的总高度约为2.2 m)乘电梯刚好安全通过,请你根据图中数据回答,两层楼之间的高度约为(

A.5.5 m
B.6.2 m
C.11 m
D.2.2 m
A
)
A.5.5 m
B.6.2 m
C.11 m
D.2.2 m
答案:
3.A [解析]如图,过点D作DE//BC交FC于点E.

∴∠EDC = ∠ACB.
∵AB//CE,
∴∠BAC = ∠DCE.
∴△ABC∽△CED.设AB = xm.根据题意,得DE = 10 - 4 = 6(m),EC = (x - 2.2)m.
∴$\frac{AB}{EC}=\frac{BC}{DE}$,即$\frac{x}{x - 2.2}=\frac{10}{6}$.解得x = 5.5.经检验,x = 5.5是原分式方程的解,且符合题意,
∴AB = 5.5m,即两层楼之间的高度约为5.5m.故选A.
3.A [解析]如图,过点D作DE//BC交FC于点E.

∴∠EDC = ∠ACB.
∵AB//CE,
∴∠BAC = ∠DCE.
∴△ABC∽△CED.设AB = xm.根据题意,得DE = 10 - 4 = 6(m),EC = (x - 2.2)m.
∴$\frac{AB}{EC}=\frac{BC}{DE}$,即$\frac{x}{x - 2.2}=\frac{10}{6}$.解得x = 5.5.经检验,x = 5.5是原分式方程的解,且符合题意,
∴AB = 5.5m,即两层楼之间的高度约为5.5m.故选A.
4.〔太原市〕图1是机场常用的一种圆锥形直饮水杯,这种设计是为了节省存储空间. 小明画出这种纸杯的截面图如图2所示,其中点O为杯底顶点,AB,CD分别表示杯口、水面,OA = OB,CD//AB. 若杯中水的高度是杯子高度的80%,则水的体积与杯子容积的比最接近于 (

A.80%
B.70%
C.64%
D.50%
图1
图2
D
)
A.80%
B.70%
C.64%
D.50%
图1
图2
答案:
4.D [解析]设杯子的高为h,则杯中水的高为$\frac{4}{5}h$.
∵CD//AB,
∴△OCD∽△OAB.
∴$\frac{CD}{AB}=\frac{\frac{4}{5}h}{h}=\frac{4}{5}$,
∴CD = $\frac{4}{5}AB$.
$\frac{\frac{1}{3}\pi· (\frac{CD}{2})^{2}· \frac{4}{5}h}{\frac{1}{3}\pi· (\frac{AB}{2})^{2}· h}=\frac{\frac{CD^{2}}{4}}{\frac{AB^{2}}{4}}=\frac{CD^{2}}{AB^{2}}=\frac{64}{125}=0.512\approx50\%$.
∴水的体积与杯子容积的比最接近于50%.故选D.
∵CD//AB,
∴△OCD∽△OAB.
∴$\frac{CD}{AB}=\frac{\frac{4}{5}h}{h}=\frac{4}{5}$,
∴CD = $\frac{4}{5}AB$.
$\frac{\frac{1}{3}\pi· (\frac{CD}{2})^{2}· \frac{4}{5}h}{\frac{1}{3}\pi· (\frac{AB}{2})^{2}· h}=\frac{\frac{CD^{2}}{4}}{\frac{AB^{2}}{4}}=\frac{CD^{2}}{AB^{2}}=\frac{64}{125}=0.512\approx50\%$.
∴水的体积与杯子容积的比最接近于50%.故选D.
5.〔北京市〕如图,在圆形花圃中有两条笔直的小路,两端都在花圃边界上,分别记为AC,BD,设交点为P,点C,D之间有一些假山,为了测量C,D之间的距离,小明已经测量了线段AP和PD的长度,只需再测量一条线段的长度,就可以计算C,D之间的距离. 小明应该测量的是 (
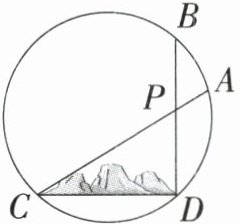
A.线段BP
B.线段CP
C.线段AB
D.线段AD
C
)
A.线段BP
B.线段CP
C.线段AB
D.线段AD
答案:
5.C [解析]连接AB.
∵∠DCP = ∠ABP,∠DPC = ∠APB,
∴△DPC∽△APB.
∴$\frac{CP}{BP}=\frac{CD}{AB}=\frac{PD}{AP}$
∵小明已经测量了线段AP和PD的长度,
∴只需再测量线段AB的长度就可以计算C,D之间的距离.故选C.
∵∠DCP = ∠ABP,∠DPC = ∠APB,
∴△DPC∽△APB.
∴$\frac{CP}{BP}=\frac{CD}{AB}=\frac{PD}{AP}$
∵小明已经测量了线段AP和PD的长度,
∴只需再测量线段AB的长度就可以计算C,D之间的距离.故选C.
6.〔郑州模拟〕凸透镜成像的原理如图所示,AG//l//HC. 若缩小的实像是物体的$\frac{2}{3}$,则物体到焦点$F_1$的距离与焦点$F_2$到凸透镜的中心线GH的距离的比值为(焦点$F_1$和$F_2$关于点O对称) (

A.$\frac{3}{2}$
B.$\frac{2}{3}$
C.2
D.$\frac{1}{2}$
A
)
A.$\frac{3}{2}$
B.$\frac{2}{3}$
C.2
D.$\frac{1}{2}$
答案:
6.A [解析]连接$HF_{2}$.根据题意,得$CD\bot l$,$HO\bot l$.
∴∠HOD = 90°.
∵l//HC,
∴HO = CD.
∵AB⊥l,
∴∠ABF₁ = 90°.
∵焦点$F_{1}$和$F_{2}$关于点O对称,
∴$HF_{1}=HF_{2}$.
∴∠$HF_{1}O$ = ∠$HF_{2}O$.
∵∠$AF_{1}B$ = ∠$HF_{1}O$,
∴∠$AF_{1}B$ = ∠$HF_{2}O$.
∵∠$ABF_{1}$ = ∠HOD = 90°,
∴△$ABF_{1}$∽△$HOF_{2}$.
∴$\frac{BF_{1}}{OF_{2}}=\frac{AB}{HO}$.
∵缩小的实像是物体的$\frac{2}{3}$,
∴$\frac{AB}{HO}=\frac{AB}{CD}=\frac{3}{2}$,
∴$\frac{BF_{1}}{OF_{2}}=\frac{3}{2}$,即物体到焦点$F_{1}$的距离与焦点$F_{2}$到凸透镜的中心线GH的距离的比值为$\frac{3}{2}$.故选A.
∴∠HOD = 90°.
∵l//HC,
∴HO = CD.
∵AB⊥l,
∴∠ABF₁ = 90°.
∵焦点$F_{1}$和$F_{2}$关于点O对称,
∴$HF_{1}=HF_{2}$.
∴∠$HF_{1}O$ = ∠$HF_{2}O$.
∵∠$AF_{1}B$ = ∠$HF_{1}O$,
∴∠$AF_{1}B$ = ∠$HF_{2}O$.
∵∠$ABF_{1}$ = ∠HOD = 90°,
∴△$ABF_{1}$∽△$HOF_{2}$.
∴$\frac{BF_{1}}{OF_{2}}=\frac{AB}{HO}$.
∵缩小的实像是物体的$\frac{2}{3}$,
∴$\frac{AB}{HO}=\frac{AB}{CD}=\frac{3}{2}$,
∴$\frac{BF_{1}}{OF_{2}}=\frac{3}{2}$,即物体到焦点$F_{1}$的距离与焦点$F_{2}$到凸透镜的中心线GH的距离的比值为$\frac{3}{2}$.故选A.
查看更多完整答案,请扫码查看


