2026年王朝霞考点梳理时习卷九年级数学全一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年王朝霞考点梳理时习卷九年级数学全一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1.〔长春市〕如图,在平面直角坐标系中,直线$y = mx + n$与抛物线$y = ax^{2} + bx + c$交于$A(-1,p)$,$B(2,q)$两点,则关于$x$的不等式$mx + n > ax^{2} + bx + c$的解集是 (
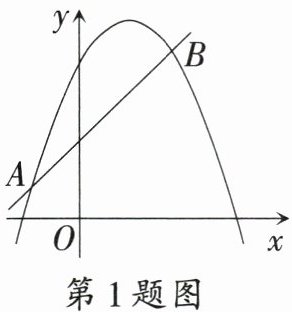
A.$x < -1$
B.$x > 2$
C.$-1 < x < 2$
D.$x < -1$或$x > 2$
D
)
A.$x < -1$
B.$x > 2$
C.$-1 < x < 2$
D.$x < -1$或$x > 2$
答案:
1.D
2. 如图,$Rt \bigtriangleup OAB$的顶点$A(-2,4)$在抛物线$y = ax^{2}$上,将$Rt \bigtriangleup OAB$绕点$O$顺时针旋转$90^{\circ}$,得到$\bigtriangleup OCD$,边$CD$与该抛物线交于点$P$,则点$P$的坐标为 (

A.$(\sqrt{2},\sqrt{2})$
B.$(\sqrt{2},2)$
C.$(2,2)$
D.$(2,\sqrt{2})$
B
)
A.$(\sqrt{2},\sqrt{2})$
B.$(\sqrt{2},2)$
C.$(2,2)$
D.$(2,\sqrt{2})$
答案:
2.B
3. 如图,平面直角坐标系内有一顶点为$A$的抛物线,与直线$y = 2$交于$B,C$两点,$\bigtriangleup ABC$为等边三角形.若点$A$坐标为$(-3,0)$,则此抛物线与$y$轴的交点坐标为 (

A.$(0,\frac{9}{2})$
B.$(0,\frac{27}{2})$
C.$(0,9)$
D.$(0,19)$
B
)
A.$(0,\frac{9}{2})$
B.$(0,\frac{27}{2})$
C.$(0,9)$
D.$(0,19)$
答案:
3.B
4. 如图,抛物线$y = x^{2} - 4x - 5$与$x$轴的负半轴交于点$B$,与$y$轴交于点$C$,点$A(a, -5)$在抛物线上.若点$E$在$y$轴上,且$\angle BEO = \angle BAC$,则点$E$的坐标为(

A.$(0,- \frac{3}{2})$
B.$(0,\frac{3}{2})$
C.$(0,1)$
D.$(0,1)$或$(0, -1)$
D
)
A.$(0,- \frac{3}{2})$
B.$(0,\frac{3}{2})$
C.$(0,1)$
D.$(0,1)$或$(0, -1)$
答案:
4.D
5. 抛物线$y = - \frac{2}{3}x^{2} + 2bx$与$x$轴的两个不同的交点分别是点$O$和点$A$,抛物线的顶点$B$在直线$y = \frac{\sqrt{3}}{3}x$上,则关于$\bigtriangleup OAB$的判断正确的是 (
A.等腰三角形
B.直角三角形
C.等边三角形
D.等腰直角三角形
A
)A.等腰三角形
B.直角三角形
C.等边三角形
D.等腰直角三角形
答案:
5.A
6. 如图,四边形$OABC$是边长为$1$的正方形,$OC$与$x$轴正半轴的夹角为$15^{\circ}$,点$B$在抛物线$y = ax^{2}(a < 0)$的图象上,则$a$的值为 (

A.$\frac{\sqrt{2}}{2}$
B.$\frac{\sqrt{2}}{3}$
C.$- \frac{\sqrt{2}}{3}$
D.$- \frac{\sqrt{2}}{2}$
C
)
A.$\frac{\sqrt{2}}{2}$
B.$\frac{\sqrt{2}}{3}$
C.$- \frac{\sqrt{2}}{3}$
D.$- \frac{\sqrt{2}}{2}$
答案:
6.C [解析]如图,连接OB,过点B作BD⊥x轴于点D.

∵四边形OABC是边长为1的正方形,
∴∠BOC = 45°,OA = AB = 1,∠A = 90°.
∴OB = $\sqrt{OA^{2}+AB^{2}}$ = $\sqrt{2}$.
∵OC与x轴正半轴的夹角为15°,
∴∠BOD = 30°.
∴BD = $\frac{1}{2}$OB = $\frac{\sqrt{2}}{2}$.
∴OD = $\sqrt{OB^{2}-BD^{2}}$ = $\frac{\sqrt{6}}{2}$.
∴点B($\frac{\sqrt{6}}{2}$, -$\frac{\sqrt{2}}{2}$)
将点B($\frac{\sqrt{6}}{2}$, -$\frac{\sqrt{2}}{2}$)代入y = ax²,
得($\frac{\sqrt{6}}{2}$)²a = -$\frac{\sqrt{2}}{2}$.
解得a = -$\frac{\sqrt{2}}{3}$.故选C.
6.C [解析]如图,连接OB,过点B作BD⊥x轴于点D.

∵四边形OABC是边长为1的正方形,
∴∠BOC = 45°,OA = AB = 1,∠A = 90°.
∴OB = $\sqrt{OA^{2}+AB^{2}}$ = $\sqrt{2}$.
∵OC与x轴正半轴的夹角为15°,
∴∠BOD = 30°.
∴BD = $\frac{1}{2}$OB = $\frac{\sqrt{2}}{2}$.
∴OD = $\sqrt{OB^{2}-BD^{2}}$ = $\frac{\sqrt{6}}{2}$.
∴点B($\frac{\sqrt{6}}{2}$, -$\frac{\sqrt{2}}{2}$)
将点B($\frac{\sqrt{6}}{2}$, -$\frac{\sqrt{2}}{2}$)代入y = ax²,
得($\frac{\sqrt{6}}{2}$)²a = -$\frac{\sqrt{2}}{2}$.
解得a = -$\frac{\sqrt{2}}{3}$.故选C.
7.〔郑州外国语中学〕如图,在等腰直角三角形$ABC$中,$\angle B = 90^{\circ}$,$AC = 4$,正方形$ADEF$中,$AF = 2$,$F,A,C$在同一直线上,正方形$ADEF$沿射线$FA$方向平移,直到点$F$与点$C$重合.若点$F$的平移距离为$x$,平移过程中两个图形重叠部分的面积为$y$,则表示$y$与$x$的关系的函数图象正确的是 (


A.
B.
C.
D.
B
)

A.
B.
C.
D.
答案:
7.B [解析]设正方形ADEF平移后的对应图形为正方形A'D'E'F'
由平移的性质知AA' = FF' = x,A'F' = AF = 2.
过点B作BG⊥AC于点G.
∵△ABC是等腰直角三角形,AC = 4,
∴BG = AG = CG = 2,∠BAC = ∠ACB = 45°.
根据题意,分三种情况:
①当0 ≤ x < 2时,设A'D'与AB交于点P.
∵∠BAC = 45°,
∴A'P = AA' = x.
∴y = S△AA'P = $\frac{1}{2}$A'P·AA' = $\frac{1}{2}$x².
②当2 ≤ x ≤ 4时,设E'F'与AB交于点H,A'D'与BC交于点Q.
∴AF' = FF' - AF = x - 2,A'C = AC - AA' = 4 - x.
∵∠BAC = ∠ACB = 45°,
∴AF' = F'H = x - 2,A'C = A'Q = 4 - x.
∴y = S△ABC - S△AF'H - S△A'QC = $\frac{1}{2}$BG·AC - $\frac{1}{2}$AF'·F'H - $\frac{1}{2}$A'C·A'Q = $\frac{1}{2}$×2×4 - $\frac{1}{2}$(x - 2)² - $\frac{1}{2}$(4 - x)² = -x² + 6x - 6.
③当4 < x ≤ 6时,设E'F'与BC交于点M.
∴CF' = A'F' - (AA' - AC) = 6 - x.

∵∠ACB = 45°,
∴CF' = MF' = 6 - x.
∴y = S△CF'M = $\frac{1}{2}$CF'·MF' = $\frac{1}{2}$(6 - x)².
综上所述,B选项符合题意故选B.
7.B [解析]设正方形ADEF平移后的对应图形为正方形A'D'E'F'
由平移的性质知AA' = FF' = x,A'F' = AF = 2.
过点B作BG⊥AC于点G.
∵△ABC是等腰直角三角形,AC = 4,
∴BG = AG = CG = 2,∠BAC = ∠ACB = 45°.
根据题意,分三种情况:
①当0 ≤ x < 2时,设A'D'与AB交于点P.
∵∠BAC = 45°,
∴A'P = AA' = x.
∴y = S△AA'P = $\frac{1}{2}$A'P·AA' = $\frac{1}{2}$x².
②当2 ≤ x ≤ 4时,设E'F'与AB交于点H,A'D'与BC交于点Q.
∴AF' = FF' - AF = x - 2,A'C = AC - AA' = 4 - x.
∵∠BAC = ∠ACB = 45°,
∴AF' = F'H = x - 2,A'C = A'Q = 4 - x.
∴y = S△ABC - S△AF'H - S△A'QC = $\frac{1}{2}$BG·AC - $\frac{1}{2}$AF'·F'H - $\frac{1}{2}$A'C·A'Q = $\frac{1}{2}$×2×4 - $\frac{1}{2}$(x - 2)² - $\frac{1}{2}$(4 - x)² = -x² + 6x - 6.
③当4 < x ≤ 6时,设E'F'与BC交于点M.
∴CF' = A'F' - (AA' - AC) = 6 - x.

∵∠ACB = 45°,
∴CF' = MF' = 6 - x.
∴y = S△CF'M = $\frac{1}{2}$CF'·MF' = $\frac{1}{2}$(6 - x)².
综上所述,B选项符合题意故选B.
查看更多完整答案,请扫码查看


