2026年王朝霞考点梳理时习卷九年级数学全一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年王朝霞考点梳理时习卷九年级数学全一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
9.〔重庆市改编〕用一个圆心角为$216^{\circ}$,半径为$10 cm$的扇形做成一个圆锥的侧面,这个圆锥的高为
8
$ cm$.
答案:
9.8
10.已知正六边形的边心距为$\sqrt{6}$,则它的外接圆半径为
2$\sqrt{2}$
.
答案:
10.2$\sqrt{2}$ [解析]如图,在正六边形中,∠AOB=60°,OA=OB.过点O作OG⊥AB于点G,则OG=$\sqrt{6}$,∠AOG=30°.
∴OA=2AG.

在Rt△AOG中,由勾股定理,得OA²=OG²+AG².
∴4AG²=6+AG².
∴AG=$\sqrt{2}$.
∴OA=2AG=2$\sqrt{2}$.
∴正六边形的外接圆半径为2$\sqrt{2}$.
10.2$\sqrt{2}$ [解析]如图,在正六边形中,∠AOB=60°,OA=OB.过点O作OG⊥AB于点G,则OG=$\sqrt{6}$,∠AOG=30°.
∴OA=2AG.

在Rt△AOG中,由勾股定理,得OA²=OG²+AG².
∴4AG²=6+AG².
∴AG=$\sqrt{2}$.
∴OA=2AG=2$\sqrt{2}$.
∴正六边形的外接圆半径为2$\sqrt{2}$.
11.〔新乡模拟〕如图,网格中的小正方形的边长均为1,点$A,B,C$都在小正方形的顶点上,点$P$为$\overset{\frown} {BC}$上一动点,连接$PB,PC$,则图中阴影部分面积的最小值为
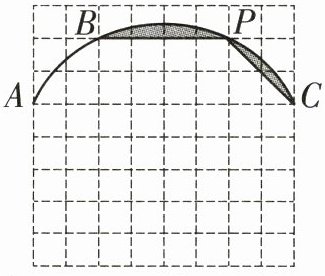
5π−10$\sqrt{2}$
.
答案:
11.5π−10$\sqrt{2}$ [解析]如图,连接AC,取AC的中点D,连接OD,OA,OB,OC,BC.

∵OD⊥AC,AD=CD,
∴OD所在直线为AC的垂直平分线.
∴AC所在圆的圆心在OD所在的直线上.
∵OA=OB=OC=$\sqrt{4^{2}+2^{2}}$=2$\sqrt{5}$,
∴点O为$\overset{\frown}{AC}$所在圆的圆心.
∵BC=$\sqrt{6^{2}+2^{2}}$=2$\sqrt{10}$,
∴OB²+OC²=BC².
∴∠BOC=90°.
∴S△BOC=$\frac{1}{2}$OB·OC=10,
S扇形OBC=$\frac{90\pi × (2\sqrt{5})^{2}}{360}$=5π.
∴S阴影=5π−10−S△BPC.
∴当S△BPC最大时,S阴影最小.
∵△BPC的边BC长为定值,
∴BC边上的高最长时,S△BPC最大.过点O作OP'⊥BC,交BC于点H,交$\overset{\frown}{BC}$于点P'.此时△BPC中BC边上的高最长,为P'H的值.
∵△BOC为等腰直角三角形,
∴OH=$\frac{1}{2}$BC=$\sqrt{10}$.
∴P'H=OP'−OH=2$\sqrt{5}$−$\sqrt{10}$.
∴S△BPC的最大值为$\frac{1}{2}× 2\sqrt{10}× (2\sqrt{5}-\sqrt{10})=10\sqrt{2}-10$.
∴阴影部分面积的最小值为5π−10−(10$\sqrt{2}$−10)=5π−10$\sqrt{2}$.
11.5π−10$\sqrt{2}$ [解析]如图,连接AC,取AC的中点D,连接OD,OA,OB,OC,BC.

∵OD⊥AC,AD=CD,
∴OD所在直线为AC的垂直平分线.
∴AC所在圆的圆心在OD所在的直线上.
∵OA=OB=OC=$\sqrt{4^{2}+2^{2}}$=2$\sqrt{5}$,
∴点O为$\overset{\frown}{AC}$所在圆的圆心.
∵BC=$\sqrt{6^{2}+2^{2}}$=2$\sqrt{10}$,
∴OB²+OC²=BC².
∴∠BOC=90°.
∴S△BOC=$\frac{1}{2}$OB·OC=10,
S扇形OBC=$\frac{90\pi × (2\sqrt{5})^{2}}{360}$=5π.
∴S阴影=5π−10−S△BPC.
∴当S△BPC最大时,S阴影最小.
∵△BPC的边BC长为定值,
∴BC边上的高最长时,S△BPC最大.过点O作OP'⊥BC,交BC于点H,交$\overset{\frown}{BC}$于点P'.此时△BPC中BC边上的高最长,为P'H的值.
∵△BOC为等腰直角三角形,
∴OH=$\frac{1}{2}$BC=$\sqrt{10}$.
∴P'H=OP'−OH=2$\sqrt{5}$−$\sqrt{10}$.
∴S△BPC的最大值为$\frac{1}{2}× 2\sqrt{10}× (2\sqrt{5}-\sqrt{10})=10\sqrt{2}-10$.
∴阴影部分面积的最小值为5π−10−(10$\sqrt{2}$−10)=5π−10$\sqrt{2}$.
12.〔杭州市〕(8分)如图所示,以$□ ABCD$的顶点$A$为圆心,$AB$长为半径作圆,分别交$AD,BC$于点$E,F$,延长$BA$交$\odot A$于点$G$.
(1)求证:$\overset{\frown} {GE} =\overset{\frown} {EF}$;
(2)若$\angle C = 120^{\circ}$,$BG = 4$,求阴影部分的面积.

(1)求证:$\overset{\frown} {GE} =\overset{\frown} {EF}$;
(2)若$\angle C = 120^{\circ}$,$BG = 4$,求阴影部分的面积.

答案:
12.解:
(1)证明:连接AF.
∵四边形ABCD是平行四边形,
∴AD//BC.
∴∠GAE=∠ABF,∠EAF=∠AFB.
∵AB=AF,
∴∠ABF=∠AFB.
∴∠GAE=∠EAF.
∴GE=EF.
(2)过点A作AH⊥BF于点H.
∵四边形ABCD是平行四边形,
∴∠C+∠ABC=180°.
∵∠C=120°,
∴∠ABC=60°.
∵AB=AF,
∴△ABF是等边三角形.
∴BH=$\frac{1}{2}$BF=$\frac{1}{2}$AB,BF=AB,∠BAF=60°.
∴∠BAH=30°.
∵BG=4,
∴BF=AB=2.
∴BH=$\frac{1}{2}$AB=1,S扇形ABF=$\frac{60\pi × 2^{2}}{360}$=$\frac{2\pi}{3}$.
∴AH=$\sqrt{AB^{2}-BH^{2}}$=$\sqrt{3}$.
∵S△ABF=$\frac{1}{2}$BF·AH=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$,
∴S阴影=S扇形ABF−S△ABF=$\frac{2\pi}{3}$−$\sqrt{3}$.
(1)证明:连接AF.
∵四边形ABCD是平行四边形,
∴AD//BC.
∴∠GAE=∠ABF,∠EAF=∠AFB.
∵AB=AF,
∴∠ABF=∠AFB.
∴∠GAE=∠EAF.
∴GE=EF.
(2)过点A作AH⊥BF于点H.
∵四边形ABCD是平行四边形,
∴∠C+∠ABC=180°.
∵∠C=120°,
∴∠ABC=60°.
∵AB=AF,
∴△ABF是等边三角形.
∴BH=$\frac{1}{2}$BF=$\frac{1}{2}$AB,BF=AB,∠BAF=60°.
∴∠BAH=30°.
∵BG=4,
∴BF=AB=2.
∴BH=$\frac{1}{2}$AB=1,S扇形ABF=$\frac{60\pi × 2^{2}}{360}$=$\frac{2\pi}{3}$.
∴AH=$\sqrt{AB^{2}-BH^{2}}$=$\sqrt{3}$.
∵S△ABF=$\frac{1}{2}$BF·AH=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$,
∴S阴影=S扇形ABF−S△ABF=$\frac{2\pi}{3}$−$\sqrt{3}$.
13.(9分)如图,在$\odot O$中,弦$BC$垂直于半径$OA$,垂足为点$E$,$D$是优弧$BC$上一点,连接$BD,AD,OC$,$\angle ADB = 30^{\circ}$.
(1)求$\angle AOC$的度数;
(2)若弦$BC = 8 cm$,求劣弧$BC$的长.

(1)求$\angle AOC$的度数;
(2)若弦$BC = 8 cm$,求劣弧$BC$的长.

答案:
13.解:
(1)连接OB.
∵OA⊥BC,
∴AB=AC.
∵∠AOB=2∠ADB=60°,
∴∠AOC=∠AOB=60°.
(2)
∵OA⊥BC,
∴BE=$\frac{1}{2}$BC=4cm.
在Rt△BOE中,∠AOB=60°,
∴∠OBC=30°.
∴OB=2OE.
∵BE²=OB²−OE²,
∴OB=$\frac{8\sqrt{3}}{3}$cm.
由
(1)知∠BOC=∠AOB+∠AOC=120°,
∴劣弧BC的长为$\frac{120\pi × \frac{8\sqrt{3}}{3}}{180}=\frac{16\sqrt{3}}{9}\pi$(cm).
(1)连接OB.
∵OA⊥BC,
∴AB=AC.
∵∠AOB=2∠ADB=60°,
∴∠AOC=∠AOB=60°.
(2)
∵OA⊥BC,
∴BE=$\frac{1}{2}$BC=4cm.
在Rt△BOE中,∠AOB=60°,
∴∠OBC=30°.
∴OB=2OE.
∵BE²=OB²−OE²,
∴OB=$\frac{8\sqrt{3}}{3}$cm.
由
(1)知∠BOC=∠AOB+∠AOC=120°,
∴劣弧BC的长为$\frac{120\pi × \frac{8\sqrt{3}}{3}}{180}=\frac{16\sqrt{3}}{9}\pi$(cm).
14.〔金华中考改编〕(10分)如图1,正五边形$ABCDE$内接于$\odot O$,阅读以下作图过程,并回答下列问题.
作法:如图2.
①作直径$AF$;
②以点$F$为圆心,$FO$的长为半径作圆弧,与$\odot O$交于点$M,N$;
③连接$AM,MN,NA$.
(1)求$\angle ABC$的度数.
(2)$\triangle AMN$是正三角形吗?请说明理由.
(3)从点$A$开始,以$DN$的长为半径,在$\odot O$上依次截取点,再依次连接这些点,得到正$n$边形,直接写出$n$的值.
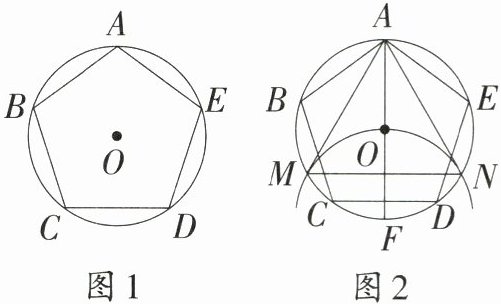
作法:如图2.
①作直径$AF$;
②以点$F$为圆心,$FO$的长为半径作圆弧,与$\odot O$交于点$M,N$;
③连接$AM,MN,NA$.
(1)求$\angle ABC$的度数.
(2)$\triangle AMN$是正三角形吗?请说明理由.
(3)从点$A$开始,以$DN$的长为半径,在$\odot O$上依次截取点,再依次连接这些点,得到正$n$边形,直接写出$n$的值.

答案:
14.解:
(1)
∵五边形ABCDE是正五边形,
∴∠ABC=$\frac{(5 - 2)× 180^{\circ}}{5}$=108°.
(2)△AMN是正三角形.
理由:连接ON,NF.
根据题意可得NF=ON=OF.
∴△FON是等边三角形.
∴∠NFA=60°.
∴∠NMA=60°.
同理可得∠ANM=60°.
∴△AMN是正三角形.
(3)n的值是15.
[解析]连接OD,ON.
∵∠NMA=60°,
∴∠AON=120°.
∵∠AOD=$\frac{360^{\circ}}{5}$×2=144°,
∴∠NOD=∠AOD−∠AON=24°.
∵360°÷24°=15,
∴n的值是15.
(1)
∵五边形ABCDE是正五边形,
∴∠ABC=$\frac{(5 - 2)× 180^{\circ}}{5}$=108°.
(2)△AMN是正三角形.
理由:连接ON,NF.
根据题意可得NF=ON=OF.
∴△FON是等边三角形.
∴∠NFA=60°.
∴∠NMA=60°.
同理可得∠ANM=60°.
∴△AMN是正三角形.
(3)n的值是15.
[解析]连接OD,ON.
∵∠NMA=60°,
∴∠AON=120°.
∵∠AOD=$\frac{360^{\circ}}{5}$×2=144°,
∴∠NOD=∠AOD−∠AON=24°.
∵360°÷24°=15,
∴n的值是15.
查看更多完整答案,请扫码查看


