《2026年王朝霞考点梳理时习卷九年级数学全一册人教版》

9.〔北京市〕如图，一次函数$y = kx + b(k \neq 0)$与二次函数$y = ax^{2}(a \neq 0 )$的图象分别交于点$A(-2,2),B(4,8)$，则关于$x$的方程$ax^{2} = kx + b$的解为x₁=−2,x₂=4.

答案： 9.x₁=−2,x₂=4

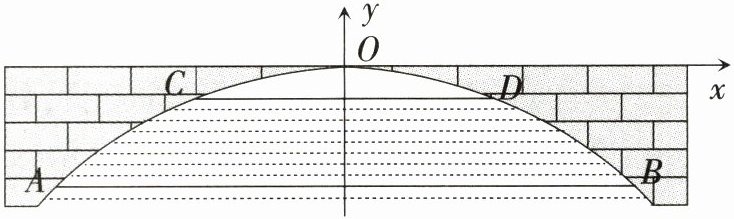
10. 教材探究改编 如图所示，一座抛物线形拱桥在正常水位时，水面$AB$宽为20 m，拱桥的最高点$O$到水面$AB$的距离为4 m. 如果此时水位上升3 m就达到警戒水位$CD$，那么$CD$宽为10m.

答案： 10. 10m

11. 如图，一段抛物线$y = -x(x - 4)(0 \leqslant x \leqslant 4)$，记为$C_{1}$，它与$x$轴交于点$O,A_{1}$. 将$C_{1}$绕点$A_{1}$顺时针旋转$180^{\circ}$得到$C_{2}$，它与$x$轴的另一交点为$A_{2}$；将$C_{2}$绕点$A_{2}$顺时针旋转$180^{\circ}$得到$C_{3}$，它与$x$轴的另一交点为$A_{3}$；$\ldots$；如此进行下去，得到一条连续的曲线. 若点$P(2026,n)$在这条曲线上，则$n$的值为4.

答案： 11.4　[解析]把y=0代入C₁:y=−x(x−4),得−x(x−4)=0.
解得x₁=0,x₂=4.
∴OA₁=4.由旋转的性质,得A₁A₂=4.
∴点A₂(8,0).
∴抛物线C₂:y=(x−4)(x−8)(4≤x≤8).
同理可得抛物线C₃:y=−(x−8)(x−12)(8≤x≤12),...,依次类推,抛物线C₅₀₇:y=−(x−4×506)(x−4×507)(2024≤x≤2028).
∴点P(2026,n)在抛物线y=−(x−4×506)(x −4×507)(2024≤x≤2028)上.
∴当x=2026时,n=−(2026−4×506)×(2026 −4×507)=4.

12. (8分)已知抛物线的解析式为$y = x^{2} - (2m - 1)x + m^{2} - m$.
(1) 求证：此抛物线与$x$轴必有两个不同的交点；
(2) 若此抛物线与直线$y = x - 3m + 4$的一个交点在$y$轴上，求$m$的值.

答案： 12.解:
(1)证明:令y=0,即x²−(2m−1)x+m²−m=0.
∵Δ=[−(2m−1)]²−4(m²−m)=1＞0,
∴方程x²−(2m−1)x+m²−m=0有两个不相等的实数根.
∴此抛物线与x轴必有两个不同的交点.(4分)
(2)在抛物线y=x²−(2m−1)x+m²−m中,
令x=0,则y=m²−m,
即抛物线与y轴的交点为(0,m²−m).
在直线y=x−3m+4中,令x=0,则y=−3m+4,即直线与y轴的交点为(0,−3m+4).　(6分)
∵该抛物线与直线y=x−3m+4的一个交点在y轴上,
∴m²−m=−3m+4.
解得m₁=−1+√5,m₂=−1−√5.　(8分)

13.〔河南中考〕(9分)从地面竖直向上发射的物体离地面的高度$h(m)$满足关系式$h = - 5t^{2} + v_{0}t$，其中$t(s)$是物体运动的时间，$v_{0}(m/s)$是物体被发射时的速度. 社团活动时，科学小组在实验楼前从地面竖直向上发射小球.
(1) 小球被发射后$\frac{v₀}{10}$$s$时离地面的高度最大(用含$v_{0}$的式子表示).
(2) 若小球离地面的最大高度为20 m，求小球被发射时的速度.
(3) 按(2)中的速度发射小球，小球离地面的高度有两次与实验楼的高度相同. 小明说：“这两次间隔的时间为3 s.”已知实验楼高15 m，请判断他的说法是否正确，并说明理由.

答案： 13.解$:(1)\frac{v₀}{10}　(3$分)
(2)根据题意,得当$t=\frac{v₀}{10}$时,h=20.
∴$-5×(\frac{v₀}{10})² + v₀×\frac{v₀}{10} = 20.$
∴v₀ = 20m/s.　(6分)
(3)小明的说法不正确.　(7分)
理由如下:由
(2),得h=−5t²+20t.
当h=15时,15=−5t²+20t.
解得t₁=1,t₂=3.
∵3−1=2(s),
∴小明的说法不正确.　(9分)