2026年王朝霞考点梳理时习卷九年级数学全一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年王朝霞考点梳理时习卷九年级数学全一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1.〔深圳市〕下图中$∠ACB$是圆心角的是
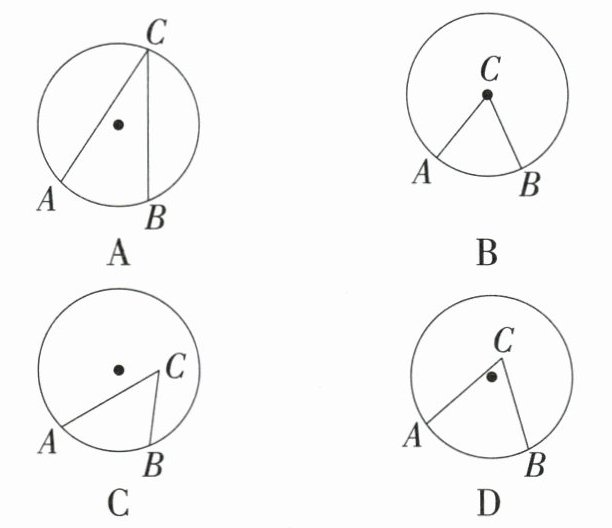
(

(
B
)
答案:
1.B
2.〔西安市〕已知$⊙O$的半径为6,则$⊙O$中弦$AB$的长度不可能是 (
A.6
B.8
C.13
D.12
C
)A.6
B.8
C.13
D.12
答案:
2.C
3.下列说法:①平分弦的直径垂直于弦;
②相等的圆心角所对的弧相等;③长度相等的两条弧是等弧;④在同圆或等圆中,如果两条弦相等,那么它们所对的圆周角相等.其中不正确的有 (
A.1个
B.2个
C.3个
D.4个
②相等的圆心角所对的弧相等;③长度相等的两条弧是等弧;④在同圆或等圆中,如果两条弦相等,那么它们所对的圆周角相等.其中不正确的有 (
D
)A.1个
B.2个
C.3个
D.4个
答案:
3.D
4. 课后题改编 用直角曲尺检查某工件,根据下列检查的结果,能判定该工件一定是半圆的是 (

B
)
答案:
4.B
5. 如图,在$⊙O$中,$AB$是直径,$CD$是弦,$AB⊥CD$,垂足为点$E$,则下列说法中正确的是
(
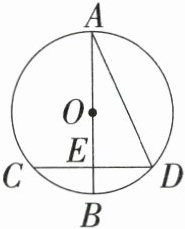
A.$AD = 2OB$
B.$B$是劣弧$CD$的中点
C.$OE = EB$
D.$D$是$\overset{\frown}{ADB}$的中点
(
B
)
A.$AD = 2OB$
B.$B$是劣弧$CD$的中点
C.$OE = EB$
D.$D$是$\overset{\frown}{ADB}$的中点
答案:
5.B
6. 以$O$为中心点的量角器与直角三角板$ABC$按如图方式摆放,量角器的0刻度线与斜边$AB$重合,点$D$为斜边$AB$上一点,作射线$CD$交弧$AB$于点$E$.如果点$E$所对应的量角器上的读数为$50°$,那么$∠ACE$的大小为
(
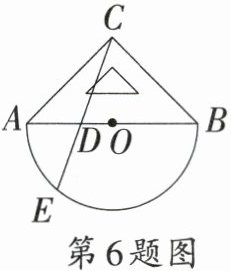
A.$20°$
B.$25°$
C.$30°$
D.$35°$
(
B
)
A.$20°$
B.$25°$
C.$30°$
D.$35°$
答案:
6.B
7.〔西安市〕如图,四边形$ABCD$为$⊙O$的内接四边形,连接$BD$.若$AB = AD = CD$,$∠BDC = 75°$,则$∠C$的度数为 (
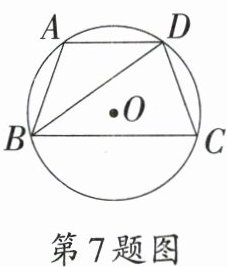
A.$55°$
B.$60°$
C.$65°$
D.$70°$
D
)
A.$55°$
B.$60°$
C.$65°$
D.$70°$
答案:
7.D [解析]
∵AB = AD = CD,
∴$\overset{\frown}{AB} = \overset{\frown}{AD} = \overset{\frown}{CD}$.
∴∠ADB = ∠ABD = ∠DBC.
设∠ADB = ∠ABD = ∠DBC = x.
∵四边形ABCD为⊙O的内接四边形,
∴∠ABC + ∠ADC = 180°,即∠ABD + ∠DBC + ∠ADB + ∠BDC = 180°.
∴3x + 75° = 180°.
解得x = 35°.
∴∠DBC = 35°.
∴∠C = 180°−∠BDC−∠DBC = 70°.故选D.
∵AB = AD = CD,
∴$\overset{\frown}{AB} = \overset{\frown}{AD} = \overset{\frown}{CD}$.
∴∠ADB = ∠ABD = ∠DBC.
设∠ADB = ∠ABD = ∠DBC = x.
∵四边形ABCD为⊙O的内接四边形,
∴∠ABC + ∠ADC = 180°,即∠ABD + ∠DBC + ∠ADB + ∠BDC = 180°.
∴3x + 75° = 180°.
解得x = 35°.
∴∠DBC = 35°.
∴∠C = 180°−∠BDC−∠DBC = 70°.故选D.
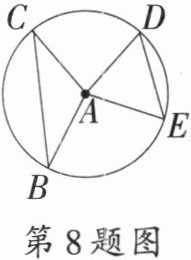
8. 如图,半径为5的$⊙A$中,弦$BC$,$ED$所对的圆心角分别是$∠BAC$,$∠EAD$.若$DE = 6$,$∠BAC + ∠EAD = 180°$,则弦$BC$的长等于
(
A.8
B.10
C.11
D.12
(
A
)
A.8
B.10
C.11
D.12
答案:
8.A [解析]如图,延长CA交⊙A于点F,连接BF.

∴∠FBC = 90°.
∵∠BAC + ∠EAD = 180°,∠BAC + ∠BAF = 180°,
∴∠EAD = ∠BAF;
∴BF = DE = 6.
∵CF = 10,
∴在Rt△CBF中,BC = $\sqrt{CF^{2}-BF^{2}}$ = 8.故选A.
8.A [解析]如图,延长CA交⊙A于点F,连接BF.

∴∠FBC = 90°.
∵∠BAC + ∠EAD = 180°,∠BAC + ∠BAF = 180°,
∴∠EAD = ∠BAF;
∴BF = DE = 6.
∵CF = 10,
∴在Rt△CBF中,BC = $\sqrt{CF^{2}-BF^{2}}$ = 8.故选A.
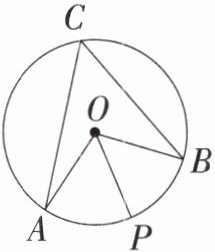
9. 如图,在$⊙O$中,$\overset{\frown}{AB}$所对的圆周角$∠ACB = 53°$.若$P$为$\overset{\frown}{AB}$上一点,$∠AOP = 56°$,则$∠POB$的度数为
50°
.
答案:
9.50°
10. 中华优秀传统文化情境 筒车 筒车是我国古代人民发明的一种水利灌溉工具.如图1,点$P$表示筒车的一个盛水桶.如图
2,当筒车工作时,盛水桶的运行路径是以轴心$O$为圆心、5 m为半径的圆,且圆心在水面上方.若圆被水面截得的弦$AB$长为8 m,则筒车工作时,盛水桶在水面以下的最大深度为
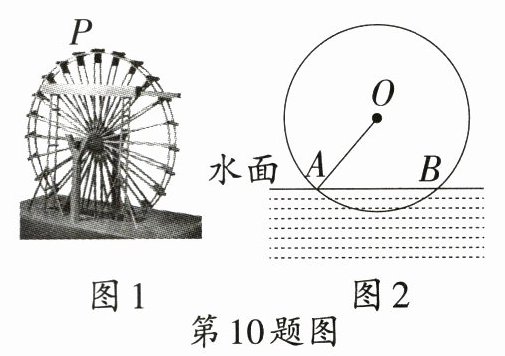
2,当筒车工作时,盛水桶的运行路径是以轴心$O$为圆心、5 m为半径的圆,且圆心在水面上方.若圆被水面截得的弦$AB$长为8 m,则筒车工作时,盛水桶在水面以下的最大深度为
2
m.
答案:
10.2 [解析]过点O作OE⊥AB于点E.
∴AE = BE = $\frac{1}{2}$AB = 4m.
∴在Rt△AEO中,OE = $\sqrt{OA^{2}-AE^{2}}$ = 3m.
∴AE = BE = $\frac{1}{2}$AB = 4m.
∴在Rt△AEO中,OE = $\sqrt{OA^{2}-AE^{2}}$ = 3m.
查看更多完整答案,请扫码查看


