2026年王朝霞考点梳理时习卷九年级数学全一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年王朝霞考点梳理时习卷九年级数学全一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
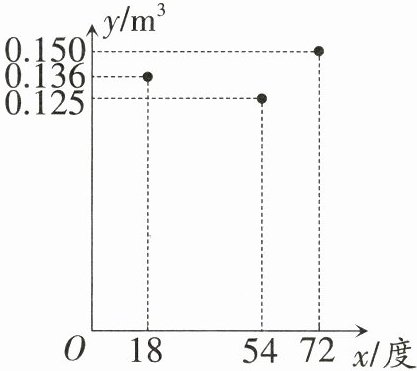
7.〔郑州模拟〕使用家用燃气灶烧开同一壶水所需的燃气量$ y $(单位:$ \mathrm{m}^{3} $)与旋钮的旋转角度$ x $(单位:度)$ (0 < x \leqslant 90) $近似满足函数关系$ y = ax^{2} + bx + c(a \neq 0) $.图中记录了某种家用节能燃气灶烧开同一壶水旋钮的旋转角度$ x $与所需燃气量$ y $的三组数据.根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮的旋转角度可能为下列选项中的 (
A.33度
B.36度
C.42度
D.49度
C
)
A.33度
B.36度
C.42度
D.49度
答案:
7.C 【解析】由题图可知,抛物线开口向上,从横坐标为18和72的两个点可以看出抛物线对称轴所在直线与x轴的交点的横坐标$x < \frac{18 + 72}{2} = 45$.
从横坐标为18和54的两个点可以看出抛物线对称轴所在直线与x轴的交点的横坐标$x > \frac{18 + 54}{2} = 36$.$\therefore$抛物线对称轴所在直线与x轴的交点的横坐标的范围是$36 < x < 45$,即对称轴位于直线$x = 36$与直线$x = 45$之间.$\therefore$此燃气灶烧开一壶水最节省燃气的旋钮的旋转角度可能为42度.故选C.
从横坐标为18和54的两个点可以看出抛物线对称轴所在直线与x轴的交点的横坐标$x > \frac{18 + 54}{2} = 36$.$\therefore$抛物线对称轴所在直线与x轴的交点的横坐标的范围是$36 < x < 45$,即对称轴位于直线$x = 36$与直线$x = 45$之间.$\therefore$此燃气灶烧开一壶水最节省燃气的旋钮的旋转角度可能为42度.故选C.
8. 课后题改编 根据有关资料,在湿滑的路面上,某汽车的刹车距离$ s(\mathrm{m}) $与车速$ v(\mathrm{km/h}) $之间满足如下关系:$ s = \dfrac{1}{100}v^{2} + \dfrac{1}{10}v $,则当汽车的刹车距离$ s $为$ 90 \mathrm{m} $时,车速$ v $为
90
$ \mathrm{km/h} $.
答案:
8.90
9. 如图,用长为$ 12 \mathrm{m} $的铝合金条制成矩形窗框,那么这个窗户的最大透光面积是

$6m^2$
(中间横框所占的面积忽略不计).
答案:
9.$6m^2$ 【解析】设窗户的高度为$x$m,面积为$S$ $m^2$,则窗户的宽为$\frac{12 - 2x}{3}$m.
根据题意,得$S = \frac{12 - 2x}{3} · x = -\frac{2}{3}x^2 + 4x = -\frac{2}{3}(x - 3)^2 + 6$.
$\therefore$当$x = 3$时,S有最大值,最大值为6.
$\therefore$这个窗户的最大透光面积为$6m^2$.
根据题意,得$S = \frac{12 - 2x}{3} · x = -\frac{2}{3}x^2 + 4x = -\frac{2}{3}(x - 3)^2 + 6$.
$\therefore$当$x = 3$时,S有最大值,最大值为6.
$\therefore$这个窗户的最大透光面积为$6m^2$.
10. (11分)某商店销售一种小兔子毛绒玩具,每件进价为30元,经过试销发现,该玩具每天的销售量$ y $(件)与销售单价$ x $(元/件)之间满足如下关系:$ y = -x + 60 $.
(1)求该商店销售这种毛绒玩具每天获得的利润$ w $(元)与$ x $(元/件)之间的函数关系式;
(2)若该商店销售这种毛绒玩具每天想获得200元的利润,且最大限度让利给顾客,则销售单价应定为多少?
(1)求该商店销售这种毛绒玩具每天获得的利润$ w $(元)与$ x $(元/件)之间的函数关系式;
(2)若该商店销售这种毛绒玩具每天想获得200元的利润,且最大限度让利给顾客,则销售单价应定为多少?
答案:
10.解:
(1)根据题意,得$w$与x之间的函数关系式为
$w = (x - 30)y$
$ = (x - 30)(-x + 60)$
$ = -x^2 + 90x - 1800$.(4分)
(2)令$-x^2 + 90x - 1800 = 200$.
解得$x_1 = 40$,$x_2 = 50$.(8分)
$\because$要最大限度让利给顾客,
$\therefore x = 40$.
答:销售单价应定为40元/件.(11分)
(1)根据题意,得$w$与x之间的函数关系式为
$w = (x - 30)y$
$ = (x - 30)(-x + 60)$
$ = -x^2 + 90x - 1800$.(4分)
(2)令$-x^2 + 90x - 1800 = 200$.
解得$x_1 = 40$,$x_2 = 50$.(8分)
$\because$要最大限度让利给顾客,
$\therefore x = 40$.
答:销售单价应定为40元/件.(11分)
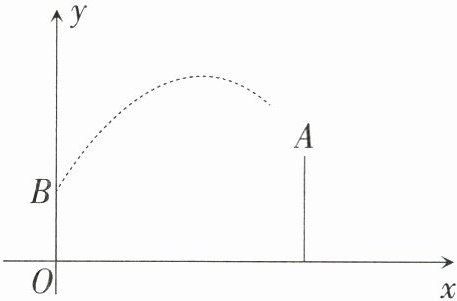
11. (12分)一名运动员第一次在距离篮圈中心$ 7 \mathrm{m} $(水平距离)远处跳起投篮,篮球在空中运行的路线为一条抛物线.球出手点$ B $距离地面$ 2 \mathrm{m} $,在与运动员水平距离为$ 4 \mathrm{m} $的空中到达最大高度$ 5.2 \mathrm{m} $,篮圈中心点$ A $距离地面约$ 3 \mathrm{m} $,建立如图所示的平面直角坐标系.
(1)求篮球运行路线所在抛物线的解析式.
(2)该运动员此次投篮篮球未经过篮圈中心,请你通过计算说明理由.
(3)该运动员在相同位置再次运球准备投篮时,吸引到对方防守人员前来拦截,该运动员立即运球后撤、跳起投篮,篮球经过篮圈中心.若该运动员在第二次投篮时的出球高度、角度和力度都与第一次一样,求他后撤的距离.
(结果保留根号)
(1)求篮球运行路线所在抛物线的解析式.
(2)该运动员此次投篮篮球未经过篮圈中心,请你通过计算说明理由.
(3)该运动员在相同位置再次运球准备投篮时,吸引到对方防守人员前来拦截,该运动员立即运球后撤、跳起投篮,篮球经过篮圈中心.若该运动员在第二次投篮时的出球高度、角度和力度都与第一次一样,求他后撤的距离.
(结果保留根号)

答案:
11.解:
(1)设篮球运行路线所在抛物线的解析式为$y = a(x - 4)^2 + 5.2$.根据题意,得点$B(0,2)$.
将点$B(0,2)$代入$y = a(x - 4)^2 + 5.2$,得$a(0 - 4)^2 + 5.2 = 2$.
解得$a = -0.2$.
$\therefore$篮球运行路线所在抛物线的解析式为$y = -0.2(x - 4)^2 + 5.2$.(4分)
(2)理由:根据题意,得点A坐标为$(7,3)$.
$\because$当$x = 7$时,$y = -0.2 × (7 - 4)^2 + 5.2 = 3.4 > 3$,
$\therefore$点A不在篮球运行路线上,即运动员此次投篮篮球未经过篮圈中心.(8分)
(3)令$y = 3$,得$-0.2(x - 4)^2 + 5.2 = 3$.
解得$x_1 = 4 + \sqrt{11}$,$x_2 = 4 - \sqrt{11}$(舍去).
$4 + \sqrt{11} - 7 = (\sqrt{11} - 3)m$.
答:他后撤的距离为$(\sqrt{11} - 3)m$.(12分)
(1)设篮球运行路线所在抛物线的解析式为$y = a(x - 4)^2 + 5.2$.根据题意,得点$B(0,2)$.
将点$B(0,2)$代入$y = a(x - 4)^2 + 5.2$,得$a(0 - 4)^2 + 5.2 = 2$.
解得$a = -0.2$.
$\therefore$篮球运行路线所在抛物线的解析式为$y = -0.2(x - 4)^2 + 5.2$.(4分)
(2)理由:根据题意,得点A坐标为$(7,3)$.
$\because$当$x = 7$时,$y = -0.2 × (7 - 4)^2 + 5.2 = 3.4 > 3$,
$\therefore$点A不在篮球运行路线上,即运动员此次投篮篮球未经过篮圈中心.(8分)
(3)令$y = 3$,得$-0.2(x - 4)^2 + 5.2 = 3$.
解得$x_1 = 4 + \sqrt{11}$,$x_2 = 4 - \sqrt{11}$(舍去).
$4 + \sqrt{11} - 7 = (\sqrt{11} - 3)m$.
答:他后撤的距离为$(\sqrt{11} - 3)m$.(12分)
查看更多完整答案,请扫码查看


