2026年王朝霞考点梳理时习卷九年级数学全一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年王朝霞考点梳理时习卷九年级数学全一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 若$y = (a + 1)x^{|a| - 2}$是反比例函数,则$a$的值是 (
A.1
B.-1
C.$\pm 1$
D.任意实数
A
)A.1
B.-1
C.$\pm 1$
D.任意实数
答案:
1.A
2.〔广州市〕下面的三个问题中都有两个变量:①面积一定的等腰三角形,底边上的高$y$与底边长$x$;②计划从$A$地到$B$地铺设一段铁轨,每日铺设长度$y$与铺设天数$x$;③将泳池中的水匀速放出,直至放完,泳池中的剩余水量$y$与放水时间$x$. 其中,变量$y$与变量$x$满足反比例函数关系的是 (
A.①②
B.①③
C.②③
D.①②③
A
)A.①②
B.①③
C.②③
D.①②③
答案:
2.A
3.〔合肥市〕若反比例函数$y = \frac{k + 2}{3}$的图象位于第二、四象限,则$k$的取值范围是 (
A.$k < 2$
B.$k < -2$
C.$k > 2$
D.$k > -2$
B
)A.$k < 2$
B.$k < -2$
C.$k > 2$
D.$k > -2$
答案:
3.B
4. 如图,正比例函数与反比例函数的图象相交于$A,B$两点,分别以点$A,B$为圆心,画与$x$轴相切的两个圆. 若点$A$的坐标为$(2,1)$,则图中阴影部分面积的和是 (
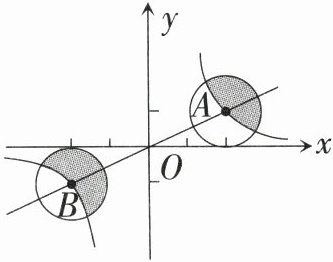
A.$\frac{1}{2}\pi$
B.$\frac{1}{4}\pi$
C.$\pi$
D.$4\pi$
C
)
A.$\frac{1}{2}\pi$
B.$\frac{1}{4}\pi$
C.$\pi$
D.$4\pi$
答案:
4.C
5.〔开封市〕下列关于反比例函数$y = -\frac{3}{x}$的结论中正确的是 (
A.图象过点$(1,3)$
B.图象在第一、三象限内
C.当$x < 0$时,$y$随$x$的增大而增大
D.当$x > -1$时,$y > 3$
C
)A.图象过点$(1,3)$
B.图象在第一、三象限内
C.当$x < 0$时,$y$随$x$的增大而增大
D.当$x > -1$时,$y > 3$
答案:
5.C
6.〔石家庄市〕函数$y = kx^2 - 2$与$y = \frac{k}{x}(k \neq 0)$在同一平面直角坐标系中的图象大致是 (
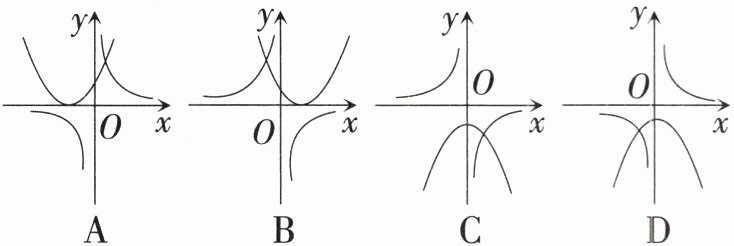
A
B
C D
C
)
A
B
C D
答案:
6.C
7.〔洛阳市〕如图,点$A,B$在反比例函数$y = \frac{k}{x}(k < 0,x < 0)$的图象上,$AD \perp x$轴于点$D$,$BE \perp x$轴于点$E$,$BC \perp y$轴于点$C$,连接$AC$. 若$OC = 1$,$OD = \frac{3}{4}OE$,$AC = AD$,则$k$的值为 (

A.-2
B.$-\frac{3\sqrt{2}}{2}$
C.-4
D.$-\frac{4\sqrt{15}}{9}$
D
)
A.-2
B.$-\frac{3\sqrt{2}}{2}$
C.-4
D.$-\frac{4\sqrt{15}}{9}$
答案:
7.D [解析]设AD与BC交于点F.
∵AD⊥x轴,BE⊥x轴,BC⊥y轴,
∴∠BEO=∠EOC=∠BCO=∠FDO=∠AFC=90°.
∴四边形BEOC与四边形FDOC均是矩形.
∴BE=DF=OC=1.
∵OD = $\frac{3}{4}$OE,
∴设OE = 4m,则OD = CF = 3m.
∴点A的横坐标为−3m,点B(−4m,1).把点B(−4m,1)代入y=$\frac{k}{x}$,得k=−4m.
∴反比例函数解析式为y=$-\frac{4m}{x}$.
∴点A(−3m,$\frac{4}{3}$).
∴AC=AD=$\frac{4}{3}$.
∴AF=AD - DF =$\frac{4}{3}-1=\frac{1}{3}$.
∵在Rt△ACF中,AC²=CF²+AF²,
∴$(\frac{4}{3})^2 = (3m)^2 + (\frac{1}{3})^2$. 解得$m_1 = \frac{\sqrt{15}}{9}$,$m_2 = -\frac{\sqrt{15}}{9}$(不符合题意,舍去).
∴k = -4m =$-\frac{4\sqrt{15}}{9}$.故选D.
∵AD⊥x轴,BE⊥x轴,BC⊥y轴,
∴∠BEO=∠EOC=∠BCO=∠FDO=∠AFC=90°.
∴四边形BEOC与四边形FDOC均是矩形.
∴BE=DF=OC=1.
∵OD = $\frac{3}{4}$OE,
∴设OE = 4m,则OD = CF = 3m.
∴点A的横坐标为−3m,点B(−4m,1).把点B(−4m,1)代入y=$\frac{k}{x}$,得k=−4m.
∴反比例函数解析式为y=$-\frac{4m}{x}$.
∴点A(−3m,$\frac{4}{3}$).
∴AC=AD=$\frac{4}{3}$.
∴AF=AD - DF =$\frac{4}{3}-1=\frac{1}{3}$.
∵在Rt△ACF中,AC²=CF²+AF²,
∴$(\frac{4}{3})^2 = (3m)^2 + (\frac{1}{3})^2$. 解得$m_1 = \frac{\sqrt{15}}{9}$,$m_2 = -\frac{\sqrt{15}}{9}$(不符合题意,舍去).
∴k = -4m =$-\frac{4\sqrt{15}}{9}$.故选D.
8. 设题新角度 开放性试题 某反比例函数$y = \frac{k}{x}$具有下列性质:当$x > 0$时,$y$随$x$的增大而减小. 写出一个满足条件的$k$的值是
1(答案不唯一)
.
答案:
8.1(答案不唯一)
查看更多完整答案,请扫码查看


