2026年王朝霞考点梳理时习卷九年级数学全一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年王朝霞考点梳理时习卷九年级数学全一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列四组图形中,不是相似图形的是 (
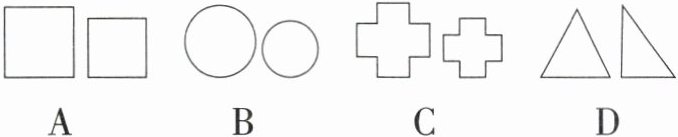
A
B
C
D
D
)
A
B
C
D
答案:
1.D
2. 在比例尺是1∶40 000的地图上,若某条道路长约为5 cm,则它的实际长度约为 (
A.0.2 km
B.2 km
C.20 km
D.200 km
B
)A.0.2 km
B.2 km
C.20 km
D.200 km
答案:
2.B
3. 〔唐山市〕下图是嘉淇作业的部分内容,其中()内应填的内容是 (

A.$D F$
B.$D E$
C.$A D$
D.$B E$
B
)
A.$D F$
B.$D E$
C.$A D$
D.$B E$
答案:
3.B
4. 将钝角三角形三条边的长度都扩大同样的倍数后得到的三角形是 (
A.钝角三角形
B.锐角三角形
C.直角三角形
D.以上都不对
A
)A.钝角三角形
B.锐角三角形
C.直角三角形
D.以上都不对
答案:
4.A
5. 〔深圳市〕若$a,b,c,d$为成比例线段,其中$a = 5 cm,b = 2.5 cm,c = 10 cm$,则线段$d$的长可能为 (
A.$2 cm$
B.$4 cm$
C.$5 cm$
D.$6 cm$
C
)A.$2 cm$
B.$4 cm$
C.$5 cm$
D.$6 cm$
答案:
5.C
6. 〔合肥市〕如图,四边形$ABCD \sim$四边形$EFGH$,$\angle A = 80°$,$\angle F = 70°$,$\angle G = 90°$,则$\angle D$等于 (

A.$70°$
B.$80°$
C.$110°$
D.$120°$
D
)
A.$70°$
B.$80°$
C.$110°$
D.$120°$
答案:
6.D
7. 〔西安市〕如图,练习本中的横格线都互相平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点$A,B,C$都在横格线上.若线段$AB = 4$,则线段$BC$长为 (

A.6
B.8
C.10
D.12
D
)
A.6
B.8
C.10
D.12
答案:
7.D
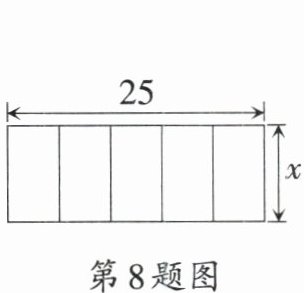
8. 矩形相邻的两条边长分别为25和$x(x<25)$,把它按如图所示的方式分割成五个全等的小矩形,每一个小矩形均与原矩形相似,则$x$的值为 (
A.5
B.$5\sqrt{5}$
C.$5\sqrt{10}$
D.10
B
)
A.5
B.$5\sqrt{5}$
C.$5\sqrt{10}$
D.10
答案:
8.B [解析]
∵原矩形的长为25,宽为x,
∴小矩形的长为x,宽为$\frac{25}{5}$=5.
∵小矩形与原矩形相似,
∴$\frac{x}{25}$=$\frac{5}{x}$.
解得$x_1$=5$\sqrt{5}$,$x_2$=−5$\sqrt{5}$(舍去).
∴x的值为5$\sqrt{5}$.故选B.
∵原矩形的长为25,宽为x,
∴小矩形的长为x,宽为$\frac{25}{5}$=5.
∵小矩形与原矩形相似,
∴$\frac{x}{25}$=$\frac{5}{x}$.
解得$x_1$=5$\sqrt{5}$,$x_2$=−5$\sqrt{5}$(舍去).
∴x的值为5$\sqrt{5}$.故选B.
9. 老师出了这样一道题目:“已知数$x,y,z$,$m$满足$\frac{x+y}{z} = \frac{y+z}{x} = \frac{x+z}{y} = m$,求$m$的值.”对于其答案,小明:$m = 2$;小红:$m = \frac{1}{2}$;小刚:$m = -1$.则正确的是 (
A.小明的答案正确
B.小明、小红的答案合在一起才完整
C.小红、小刚的答案合在一起才完整
D.小明、小刚的答案合在一起才完整
D
)A.小明的答案正确
B.小明、小红的答案合在一起才完整
C.小红、小刚的答案合在一起才完整
D.小明、小刚的答案合在一起才完整
答案:
9.D [解析]分两种情况:
①当x+y+z≠0时,
∵$\frac{x+y}{z}$=$\frac{y+z}{x}$=$\frac{x+z}{y}$=m,
∴x+y=mz,y+z=mx,x+z=my.
∴x+y+y+z+x+z=mz+mx+my,
即2(x+y+z)=m(x+y+z).
∴m=2.
②当x+y+z=0时,z=−(x+y),
∴m=$\frac{x+y}{z}$=$\frac{x+y}{−(x+y)}$=−1.
综上所述,m的值为2或−1,即小明、小刚的答案合在一起才完整.故选D.
①当x+y+z≠0时,
∵$\frac{x+y}{z}$=$\frac{y+z}{x}$=$\frac{x+z}{y}$=m,
∴x+y=mz,y+z=mx,x+z=my.
∴x+y+y+z+x+z=mz+mx+my,
即2(x+y+z)=m(x+y+z).
∴m=2.
②当x+y+z=0时,z=−(x+y),
∴m=$\frac{x+y}{z}$=$\frac{x+y}{−(x+y)}$=−1.
综上所述,m的值为2或−1,即小明、小刚的答案合在一起才完整.故选D.
10. 如图是两片形状相同的枫叶图案,则$x$的值为

11
.
答案:
10.11
查看更多完整答案,请扫码查看


