2026年王朝霞考点梳理时习卷九年级数学全一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年王朝霞考点梳理时习卷九年级数学全一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 四个等圆与直线$l$的位置关系如图所示,其中与直线$l$是相离关系的圆是 (
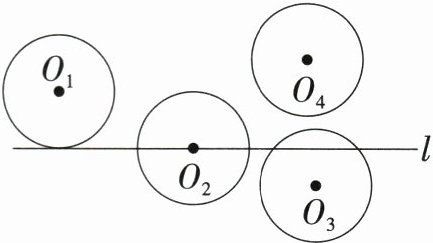
A.⊙$O_1$
B.⊙$O_2$
C.⊙$O_3$
D.⊙$O_4$
D
)
A.⊙$O_1$
B.⊙$O_2$
C.⊙$O_3$
D.⊙$O_4$
答案:
1.D
2. 已知$\triangle ABC$中,$AB=AC$,求证:$\angle B<90°$. 运用反证法证明这个结论,第一步应先假设 (
A.$\angle B\geq90°$
B.$\angle B>90°$
C.$\angle A>90°$
D.$\angle A\geq90°$
A
)A.$\angle B\geq90°$
B.$\angle B>90°$
C.$\angle A>90°$
D.$\angle A\geq90°$
答案:
2.A
3. 〔金华模拟〕在平面直角坐标系中,若⊙$A$的半径为5,点$A$的坐标是$(4,0)$,点$P$的坐标是$(0,3)$,则点$P$与⊙$A$的位置关系是 (
A.点$P$在⊙$A$内
B.点$P$在⊙$A$外
C.点$P$在⊙$A$上
D.不能确定
C
)A.点$P$在⊙$A$内
B.点$P$在⊙$A$外
C.点$P$在⊙$A$上
D.不能确定
答案:
3.C
4. 如图,$OA$交⊙$O$于点$B$,$AD$切⊙$O$于点$D$,点$C$在⊙$O$上.若$\angle A=40°$,则$\angle C$的度数为 (
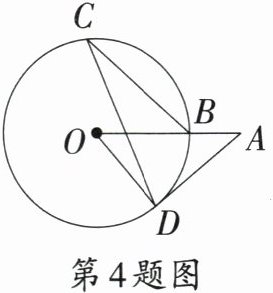
A.$40°$
B.$25°$
C.$20°$
D.$15°$
B
)
A.$40°$
B.$25°$
C.$20°$
D.$15°$
答案:
4.B
5. 小明同学用一把直尺和一个直角三角板(有一个锐角为$60°$)测量一个圆盘的直径,他把直尺、三角板和圆盘按如图的方式放置,点$A$是$60°$角顶点,点$B$是圆盘与直尺的公共点,测得$AB=3$,则此圆盘的直径为 (
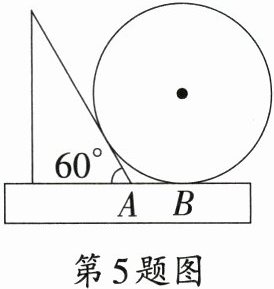
A.3
B.$2\sqrt{3}$
C.$3\sqrt{3}$
D.$6\sqrt{3}$
D
)
A.3
B.$2\sqrt{3}$
C.$3\sqrt{3}$
D.$6\sqrt{3}$
答案:
5.D
6. 如图,$\triangle ABC$的内心为点$I$,连接$AI$并延长交$\triangle ABC$的外接圆于点$D$,则线段$DI$与$DB$的关系是 (
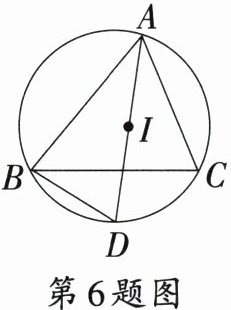
A.$DI=DB$
B.$DI>DB$
C.$DI<DB$
D.不确定
A
)
A.$DI=DB$
B.$DI>DB$
C.$DI<DB$
D.不确定
答案:
6.A [解析]连接BI,如图.

∵△ABC的内心为点I,
∴∠1 = ∠2,∠5 = ∠6.
∵∠3 = ∠1,
∴∠3 = ∠2.
∵∠4 = ∠2 + ∠6 = ∠3 + ∠5,即∠4 = ∠DBI,
∴DI = DB.故选A.
6.A [解析]连接BI,如图.

∵△ABC的内心为点I,
∴∠1 = ∠2,∠5 = ∠6.
∵∠3 = ∠1,
∴∠3 = ∠2.
∵∠4 = ∠2 + ∠6 = ∠3 + ∠5,即∠4 = ∠DBI,
∴DI = DB.故选A.
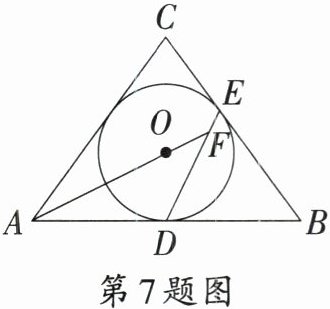
7. 如图,在$\triangle ABC$中,$\angle ACB=70°$,$\triangle ABC$的内切圆⊙$O$与$AB$,$BC$分别相切于点$D$,$E$,连接$DE$,$AO$的延长线交$DE$于点$F$,则$\angle AFD$的大小是 (
A.$35°$
B.$40°$
C.$45°$
D.$50°$
A
)
A.$35°$
B.$40°$
C.$45°$
D.$50°$
答案:
7.A [解析]
∵⊙O是△ABC的内切圆,与AB,BC分别相切于点D,E,AO平分∠BAC.
∴BE = BD,AO平分∠BAC.
∴∠BDE = ∠BED = $\frac{1}{2}$(180° - ∠B),∠DAO = $\frac{1}{2}$∠BAC.
∴∠AFD = ∠BDE - ∠DAO = $\frac{1}{2}$(180° - ∠B) - $\frac{1}{2}$∠BAC = $\frac{1}{2}$(180° - ∠B - ∠BAC).
∵180° - ∠B - ∠BAC = ∠ACB = 70°,
∴∠AFD = $\frac{1}{2}$×70° = 35°.故选A.
∵⊙O是△ABC的内切圆,与AB,BC分别相切于点D,E,AO平分∠BAC.
∴BE = BD,AO平分∠BAC.
∴∠BDE = ∠BED = $\frac{1}{2}$(180° - ∠B),∠DAO = $\frac{1}{2}$∠BAC.
∴∠AFD = ∠BDE - ∠DAO = $\frac{1}{2}$(180° - ∠B) - $\frac{1}{2}$∠BAC = $\frac{1}{2}$(180° - ∠B - ∠BAC).
∵180° - ∠B - ∠BAC = ∠ACB = 70°,
∴∠AFD = $\frac{1}{2}$×70° = 35°.故选A.
8. 数学思想 分类讨论 如图,半圆的圆心与坐标原点重合,半圆的半径为1,直线$l$的解析式为$y=x+t$.若直线$l$与半圆只有一个交点,则$t$的取值范围是 (

A.$-1<t<1$
B.$-1\leq t<1$
C.$-1<t<\sqrt{2}$
D.$t=\sqrt{2}$或$-1\leq t<1$
D
)
A.$-1<t<1$
B.$-1\leq t<1$
C.$-1<t<\sqrt{2}$
D.$t=\sqrt{2}$或$-1\leq t<1$
答案:
8.D [解析]如图.把x = 0代入y = x + t,得y = t.
∴点M(0,t).
∴OM = |t|.把y = 0代入y = x + t,得x + t = 0.解得x = -t.
∴点N(-t,0).
∴ON = |t|.
∴OM = ON.
∵∠MON = 90°,
∴∠OMN = ∠ONM = 45°.

由图可知,当直线l与半圆相切时或直线l从过点A开始平移到过点B的过程中(不包括直线l过点A),直线l与半圆只有一个交点.设直线l与半圆相切于点C,则∠OCE = 90°.
∵EF // MN,
∴∠FEO = ∠OMN = 45°.
∴∠COE = 45°.
∴CE = OC = 1.
∴OE = $\sqrt{OC² + CE²}$ = $\sqrt{2}$.
∴点E(0,$\sqrt{2}$).
把点E(0,$\sqrt{2}$)代入y = x + t,得t = $\sqrt{2}$.
∵OA = OB = 1,
∴点A(-1,0),B(1,0).当直线l分别经过点A,B时,把点A(-1,0)代入y = x + t,得-1 + t = 0.解得t = 1.把点B(1,0)代入y = x + t,得1 + t = 0.解得t = -1.由图可知当-1 ≤ t < 1时,直线l与半圆只有一个交点.综上所述,若直线l与半圆只有一个交点,则t的取值范围是t = $\sqrt{2}$或-1 ≤ t < 1.故选D.
8.D [解析]如图.把x = 0代入y = x + t,得y = t.
∴点M(0,t).
∴OM = |t|.把y = 0代入y = x + t,得x + t = 0.解得x = -t.
∴点N(-t,0).
∴ON = |t|.
∴OM = ON.
∵∠MON = 90°,
∴∠OMN = ∠ONM = 45°.

由图可知,当直线l与半圆相切时或直线l从过点A开始平移到过点B的过程中(不包括直线l过点A),直线l与半圆只有一个交点.设直线l与半圆相切于点C,则∠OCE = 90°.
∵EF // MN,
∴∠FEO = ∠OMN = 45°.
∴∠COE = 45°.
∴CE = OC = 1.
∴OE = $\sqrt{OC² + CE²}$ = $\sqrt{2}$.
∴点E(0,$\sqrt{2}$).
把点E(0,$\sqrt{2}$)代入y = x + t,得t = $\sqrt{2}$.
∵OA = OB = 1,
∴点A(-1,0),B(1,0).当直线l分别经过点A,B时,把点A(-1,0)代入y = x + t,得-1 + t = 0.解得t = 1.把点B(1,0)代入y = x + t,得1 + t = 0.解得t = -1.由图可知当-1 ≤ t < 1时,直线l与半圆只有一个交点.综上所述,若直线l与半圆只有一个交点,则t的取值范围是t = $\sqrt{2}$或-1 ≤ t < 1.故选D.
9. 如图,$\triangle ABC$内接于⊙$O$,$AB$是⊙$O$的直径,$BD$是⊙$O$的切线,点$B$为切点,$BD$与线段$AC$的延长线相交于点$D$.若$\angle ABC=65°$,则$\angle D$等于

65°
.
答案:
9.65°
查看更多完整答案,请扫码查看


