2026年王朝霞考点梳理时习卷九年级数学全一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年王朝霞考点梳理时习卷九年级数学全一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
8. 将油箱注满$k\ L$油后,轿车行驶的总路程$s$(单位:km)与平均耗油量$a$(单位:L/km)之间的反比例函数关系式为$s = \frac{k}{a} $($k$是常数,且$k \neq 0$).已知某轿车油箱注满油后,若平均耗油量为0.1 L/km,可行驶760 km,则当平均耗油量为0.08 L/km时,该轿车可以行驶
950
km.
答案:
8.950
9. 心理学家研究发现,一般情况下,在一节40 min的课堂中,学生的注意力随教师讲课时间的变化而变化.经过实验分析可知,学生的注意力指数$y$随时间$x$(min)的变化规律如图所示,其中$AB$,$BC$为线段,$CD$为双曲线的一部分.上课开始时,注意力指数为20,第10 min时,注意力指数为40.根据图象信息,若开始上课第$x$ min学生的注意力指数与下课时($x = 40$)的注意力指数相等,则$x$的值为

2.5
.
答案:
9.2.5 【解析】
∵点$A(0,20)$,
∴设线段$AB$所在直线的解析式为$y_1 = k_1x + 20$. 把点$B(10,40)$代入,得$10k_1 + 20 = 40$. 解得$k_1 = 2$.
∴线段$AB$所在直线的解析式为$y_1 = 2x + 20 ( 0 \leq x \leq 10 )$. 设点$C,D$所在双曲线的解析式为$y_2 = \frac { k_2 } { x }$. 把点$C(25,40)$代入,得$k_2 = 25 × 40 = 1 000$.
∴点$C,D$所在双曲线的解析式为$y_2 = \frac { 1 000 } { x } ( 25 \leq x \leq 40 )$.
∴当$x = 40$时,$y_2 = \frac { 1 000 } { 40 } = 25$,即下课时学生注意力指数为25.若开始上课第$x min$学生的注意力指数与下课时的注意力指数相等,则$2x + 20 = 25$.解得$x = 2.5$.
∵点$A(0,20)$,
∴设线段$AB$所在直线的解析式为$y_1 = k_1x + 20$. 把点$B(10,40)$代入,得$10k_1 + 20 = 40$. 解得$k_1 = 2$.
∴线段$AB$所在直线的解析式为$y_1 = 2x + 20 ( 0 \leq x \leq 10 )$. 设点$C,D$所在双曲线的解析式为$y_2 = \frac { k_2 } { x }$. 把点$C(25,40)$代入,得$k_2 = 25 × 40 = 1 000$.
∴点$C,D$所在双曲线的解析式为$y_2 = \frac { 1 000 } { x } ( 25 \leq x \leq 40 )$.
∴当$x = 40$时,$y_2 = \frac { 1 000 } { 40 } = 25$,即下课时学生注意力指数为25.若开始上课第$x min$学生的注意力指数与下课时的注意力指数相等,则$2x + 20 = 25$.解得$x = 2.5$.
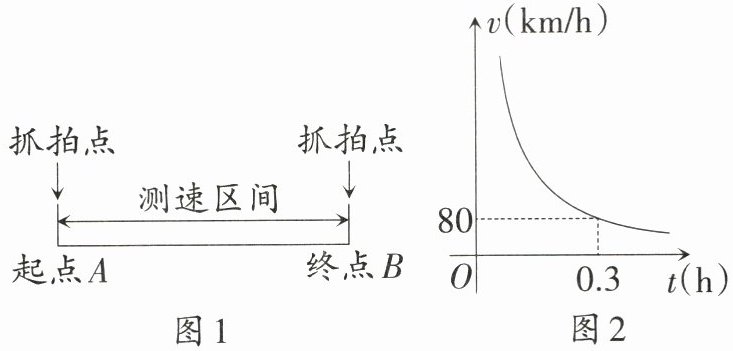
10.〔长春市〕(11分)如图1,区间测速是指检测机动车在两个相邻测速监控点之间的路段(测速区间)上的平均速度.小颖发现在安全驾驶且不超过限速的条件下,汽车在某一高速路的测速区间$AB$段的平均行驶速度$v$(单位:km/h)与行驶时间$t$(单位:h)之间满足反比例函数关系(如图2).
(1) 求$v$与$t$之间的函数解析式;
(2) 已知在测速区间$AB$上行驶的小型载客汽车的最高车速不得超过120 km/h,最低车速不得低于80 km/h,求小颖的爸爸(驾驶小型载客汽车)按照此规定通过该测速区间$AB$段的时间范围.
(1) 求$v$与$t$之间的函数解析式;
(2) 已知在测速区间$AB$上行驶的小型载客汽车的最高车速不得超过120 km/h,最低车速不得低于80 km/h,求小颖的爸爸(驾驶小型载客汽车)按照此规定通过该测速区间$AB$段的时间范围.

答案:
10.解:
(1)设$v$与$t$之间的函数解析式为$v = \frac { k } { t }$. 将$(0.3,80)$代入$v = \frac { k } { t }$,得$k = 0.3 × 80 = 24$.
∴$v = \frac { 24 } { t }$. (6分)
(2)当$v = 120$时,$ \frac { 24 } { t } = 120$.
∴$t = 0.2$.
∴小颖的爸爸按照此规定通过该测速区间$AB$段的时间范围为$0.2 \leq t \leq 0.3$. (11分)
(1)设$v$与$t$之间的函数解析式为$v = \frac { k } { t }$. 将$(0.3,80)$代入$v = \frac { k } { t }$,得$k = 0.3 × 80 = 24$.
∴$v = \frac { 24 } { t }$. (6分)
(2)当$v = 120$时,$ \frac { 24 } { t } = 120$.
∴$t = 0.2$.
∴小颖的爸爸按照此规定通过该测速区间$AB$段的时间范围为$0.2 \leq t \leq 0.3$. (11分)
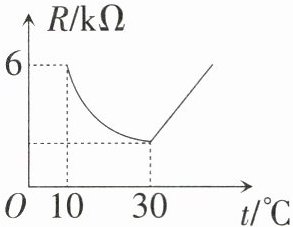
11. (12分)家用电灭蚊器的发热部分使用了某种发热材料,在一定范围内它的电阻$R$($ k\Omega$ )随温度$t$($℃$ )变化的大致图象如图所示.通电后,发热材料的温度在由$10\ ℃$上升到$30\ ℃$的过程中,电阻与温度成反比例关系,且在温度达到$30\ ℃$时,电阻下降到最小值;随后电阻随温度升高而增加,温度每上升$1\ ℃$,电阻增加$\frac{4}{15}\ k\Omega$.
(1) 求$R$($ k\Omega$ )和$t$($℃$ )之间的关系式;
(2) 家用电灭蚊器在使用过程中,温度在什么范围内时,发热材料的电阻不超过$4\ k\Omega$?
(1) 求$R$($ k\Omega$ )和$t$($℃$ )之间的关系式;
(2) 家用电灭蚊器在使用过程中,温度在什么范围内时,发热材料的电阻不超过$4\ k\Omega$?

答案:
11.解:
(1)当$10 \leq t \leq 30$时,设$R = \frac { k } { t }$. 将$(10,6)$代入,得$k = 60$.
∴$R = \frac { 60 } { t }$. (3分)
当$t = 30$时,$R = 2$.
当$t > 30$时,设$R = \frac { 4 } { 1 5 } t + b$. 将$(30,2)$代入,得$\frac { 4 } { 1 5 } × 30 + b = 2$. 解得$b = -6$.
∴$R = \frac { 4 } { 1 5 } t - 6$. (6分)
$R = \begin{cases} \frac { 60 } { t } , ( 1 0 \leq t \leq 3 0 ) \\ \frac { 4 } { 1 5 } t - 6 . ( t > 3 0 ) \end{cases} $(7分)
(2)在$R = \frac { 60 } { t }$中,令$R = 4$,得$t = 15$;
在$R = \frac { 4 } { 1 5 } t - 6$中,令$R = 4$,得$t = 37.5$. (10分)
结合题图可得,当温度$t(° C)$满足$15 \leq t \leq 37.5$时,发热材料的电阻不超过$4 k \Omega$. (12分)
(1)当$10 \leq t \leq 30$时,设$R = \frac { k } { t }$. 将$(10,6)$代入,得$k = 60$.
∴$R = \frac { 60 } { t }$. (3分)
当$t = 30$时,$R = 2$.
当$t > 30$时,设$R = \frac { 4 } { 1 5 } t + b$. 将$(30,2)$代入,得$\frac { 4 } { 1 5 } × 30 + b = 2$. 解得$b = -6$.
∴$R = \frac { 4 } { 1 5 } t - 6$. (6分)
$R = \begin{cases} \frac { 60 } { t } , ( 1 0 \leq t \leq 3 0 ) \\ \frac { 4 } { 1 5 } t - 6 . ( t > 3 0 ) \end{cases} $(7分)
(2)在$R = \frac { 60 } { t }$中,令$R = 4$,得$t = 15$;
在$R = \frac { 4 } { 1 5 } t - 6$中,令$R = 4$,得$t = 37.5$. (10分)
结合题图可得,当温度$t(° C)$满足$15 \leq t \leq 37.5$时,发热材料的电阻不超过$4 k \Omega$. (12分)
查看更多完整答案,请扫码查看


