2026年王朝霞考点梳理时习卷九年级数学全一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年王朝霞考点梳理时习卷九年级数学全一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 已知$\triangle ABC \sim \triangle DEF$,$\frac{AB}{DE} = \frac{1}{2}$,若$AC = 3$,则$DF =$ (
A.6
B.4
C.16
D.8
A
)A.6
B.4
C.16
D.8
答案:
1.A
2.〔芜湖市〕如图,四边形$ABCD$的对角线$CA$平分$\angle BCD$,补充下列条件后仍不能判定$\triangle ADC$和$\triangle BAC$相似的是 (
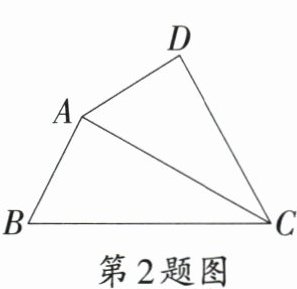
A.$\angle ADC = \angle BAC$
B.$\angle DAC = \angle ABC$
C.$AC^{2} = BC · CD$
D.$\frac{AD}{CD} = \frac{AB}{AC}$
D
)
A.$\angle ADC = \angle BAC$
B.$\angle DAC = \angle ABC$
C.$AC^{2} = BC · CD$
D.$\frac{AD}{CD} = \frac{AB}{AC}$
答案:
2.D
3.〔北京市〕如图,将$\triangle ABC$沿$BC$方向平移至$\triangle DEF$,点$A,B,C$的对应点分别是$D,E,F$,使得$BC:EC = 5:3$,则$\triangle ABC$与$\triangle GEC$的周长之比为 (
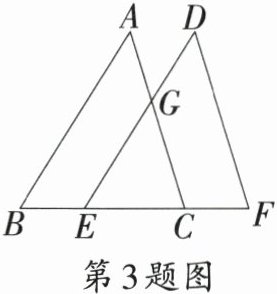
A.$2:3$
B.$2:5$
C.$5:3$
D.$3:5$
C
)
A.$2:3$
B.$2:5$
C.$5:3$
D.$3:5$
答案:
3.C
4. 在$\triangle ABC$与$\triangle DEF$中,$\angle A = \angle D = 60^{\circ}$,$\frac{AB}{DF} = \frac{AC}{DE}$.如果$\angle B = 50^{\circ}$,那么$\angle E$的度数是 (
A.$50^{\circ}$
B.$60^{\circ}$
C.$70^{\circ}$
D.$80^{\circ}$
C
)A.$50^{\circ}$
B.$60^{\circ}$
C.$70^{\circ}$
D.$80^{\circ}$
答案:
4.C
5. 如图,在$\triangle ABC$中,$\angle A = 78^{\circ}$,$AB = 4$,$AC = 6$,将$\triangle ABC$沿图示中的虚线剪开,剪下的阴影三角形与原三角形不一定相似的是 (


B
)

答案:
5.B
6.〔西安市〕如图,在等边三角形$ABC$中,点$D,E$分别是$BC,AC$上的点,$\angle ADE = 60^{\circ}$,$AB = 4$,$CD = 1$,则$AE =$ (
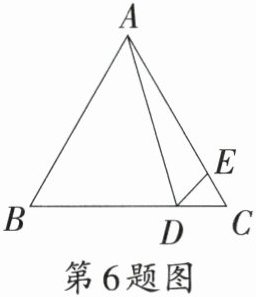
A.3
B.$\frac{15}{4}$
C.$\frac{7}{2}$
D.$\frac{13}{4}$
D
)
A.3
B.$\frac{15}{4}$
C.$\frac{7}{2}$
D.$\frac{13}{4}$
答案:
6.D
一题多解
方法一:
∵△ABC为等边三角形,
∴AB=BC=AC=4,∠B=∠C=60°。
∵CD=1,
∴BD=BC - CD=3。
∵∠ADC=∠BAD+∠B=∠ADE+∠CDE,
∠ADE=∠B=60°,
∴∠BAD=∠CDE。
∴△ABD∽△DCE。
∴$\frac{AB}{CD}=\frac{BD}{CE}$,即$\frac{4}{1}=\frac{3}{CE}$
∴$CE=\frac{3}{4}$。
∴AE=AC - CE=$4-\frac{3}{4}=\frac{13}{4}$。故选D。
方法二:过点A作AF⊥BC于点F。
∵△ABC是等边三角形,
∴AB=BC=AC=4,∠B=∠C=60°。
∵AF⊥BC,
∴∠BAF=30°,BF=CF=$\frac{1}{2}$BC=2。
∴$AF=\sqrt{AB^{2}-BF^{2}}=2\sqrt{3}$。
∵CD=1,
∴DF=1。
∴$AD=\sqrt{AF^{2}+DF^{2}}=\sqrt{13}$。
∵∠ADE=∠C=60°,∠DAE=∠CAD,
∴△ADE∽△ACD。
∴$\frac{AE}{AD}=\frac{AD}{AC}$,即$\frac{AE}{\sqrt{13}}=\frac{\sqrt{13}}{4}$。
∴$AE=\frac{13}{4}$。故选D。
一题多解
方法一:
∵△ABC为等边三角形,
∴AB=BC=AC=4,∠B=∠C=60°。
∵CD=1,
∴BD=BC - CD=3。
∵∠ADC=∠BAD+∠B=∠ADE+∠CDE,
∠ADE=∠B=60°,
∴∠BAD=∠CDE。
∴△ABD∽△DCE。
∴$\frac{AB}{CD}=\frac{BD}{CE}$,即$\frac{4}{1}=\frac{3}{CE}$
∴$CE=\frac{3}{4}$。
∴AE=AC - CE=$4-\frac{3}{4}=\frac{13}{4}$。故选D。
方法二:过点A作AF⊥BC于点F。
∵△ABC是等边三角形,
∴AB=BC=AC=4,∠B=∠C=60°。
∵AF⊥BC,
∴∠BAF=30°,BF=CF=$\frac{1}{2}$BC=2。
∴$AF=\sqrt{AB^{2}-BF^{2}}=2\sqrt{3}$。
∵CD=1,
∴DF=1。
∴$AD=\sqrt{AF^{2}+DF^{2}}=\sqrt{13}$。
∵∠ADE=∠C=60°,∠DAE=∠CAD,
∴△ADE∽△ACD。
∴$\frac{AE}{AD}=\frac{AD}{AC}$,即$\frac{AE}{\sqrt{13}}=\frac{\sqrt{13}}{4}$。
∴$AE=\frac{13}{4}$。故选D。
7. 如图,在菱形$ABCD$中,点$E,F$分别是边$AB,AD$的中点,连接$CE,CF$,分别交对角线$BD$于点$M,N$,连接$EF$,则$BN:EF$等于 (
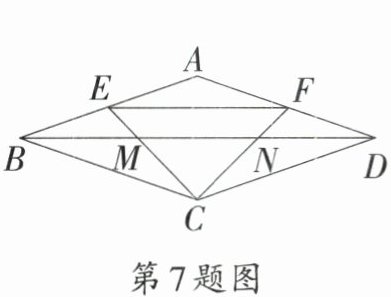
A.$1:1$
B.$1:2$
C.$4:3$
D.$3:2$
C
)
A.$1:1$
B.$1:2$
C.$4:3$
D.$3:2$
答案:
7.C [解析]
∵四边形ABCD是菱形,
∴AD=BC,AD//BC。
∴△DFN∽△BCN。
∵E,F分别是边AB,AD的中点,
∴BD=2EF,BC=2DF。
∴$\frac{DF}{BC}=\frac{DN}{BN}=\frac{1}{2}$。
∴$BN=\frac{2}{3}BD$。
∵BD=2EF,
∴$BN=\frac{4}{3}EF$。
∴BN:EF=4:3。故选C。
∵四边形ABCD是菱形,
∴AD=BC,AD//BC。
∴△DFN∽△BCN。
∵E,F分别是边AB,AD的中点,
∴BD=2EF,BC=2DF。
∴$\frac{DF}{BC}=\frac{DN}{BN}=\frac{1}{2}$。
∴$BN=\frac{2}{3}BD$。
∵BD=2EF,
∴$BN=\frac{4}{3}EF$。
∴BN:EF=4:3。故选C。
8.〔平顶山市〕如图,在平面直角坐标系中,$O$为原点,四边形$OABC$为矩形,且点$C$的坐标为$(-1,2)$,点$B$的纵坐标为$\frac{7}{2}$,则点$A$的坐标为 (

A.$(3,\frac{3}{2})$
B.$(2,\frac{3}{2})$
C.$(3,\frac{9}{4})$
D.$(4,2)$
A
)
A.$(3,\frac{3}{2})$
B.$(2,\frac{3}{2})$
C.$(3,\frac{9}{4})$
D.$(4,2)$
答案:
8.A [解析]如图,过点C作CE⊥x轴于点E,过点B作BD⊥直线CE于点D,过点A作AH⊥x轴于点H。

∴∠AHO=∠CEO=∠BDC=90°。
∵点C( - 1,2),点B的纵坐标为$\frac{7}{2}$,
∴CE=2,OE=1,$DE=\frac{7}{2}$。
∴$CD=DE - CE=\frac{7}{2}-2=\frac{3}{2}$。
∵四边形OABC为矩形,
∴∠OCB=∠AOC=90°,AO=BC。
∵∠BCD+∠OCE=90°,∠BCD+∠CBD=90°,
∴∠CBD=∠OCE。
∴△CBD∽△OCE。
∴$\frac{CD}{OE}=\frac{BD}{CE}$
$\frac{\frac{3}{2}}{1}=\frac{BD}{2}$。
∴BD=3。
∵∠OCE+∠COE=90°,∠AOH+∠COE=90°,
∴∠OCE=∠AOH。
∵∠CBD=∠OCE,
∴∠AOH=∠CBD。
∵AO=BC,∠AHO=∠BDC=90°,
∴△AOH≌△CBD。
∴$AH=CD=\frac{3}{2},OH=BD=3$。
∴点A的坐标为$(3,\frac{3}{2})$。故选A。
8.A [解析]如图,过点C作CE⊥x轴于点E,过点B作BD⊥直线CE于点D,过点A作AH⊥x轴于点H。

∴∠AHO=∠CEO=∠BDC=90°。
∵点C( - 1,2),点B的纵坐标为$\frac{7}{2}$,
∴CE=2,OE=1,$DE=\frac{7}{2}$。
∴$CD=DE - CE=\frac{7}{2}-2=\frac{3}{2}$。
∵四边形OABC为矩形,
∴∠OCB=∠AOC=90°,AO=BC。
∵∠BCD+∠OCE=90°,∠BCD+∠CBD=90°,
∴∠CBD=∠OCE。
∴△CBD∽△OCE。
∴$\frac{CD}{OE}=\frac{BD}{CE}$
$\frac{\frac{3}{2}}{1}=\frac{BD}{2}$。
∴BD=3。
∵∠OCE+∠COE=90°,∠AOH+∠COE=90°,
∴∠OCE=∠AOH。
∵∠CBD=∠OCE,
∴∠AOH=∠CBD。
∵AO=BC,∠AHO=∠BDC=90°,
∴△AOH≌△CBD。
∴$AH=CD=\frac{3}{2},OH=BD=3$。
∴点A的坐标为$(3,\frac{3}{2})$。故选A。
9. 如图,在正方形网格中,$\triangle ABC$和$\triangle DEF$的顶点都在格点上,则$\angle BAC$的度数为
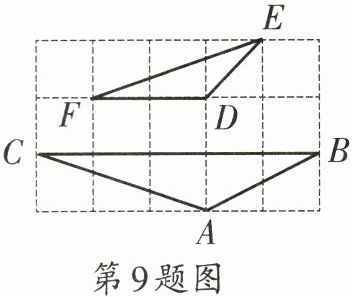
135°
.
答案:
9.135°
查看更多完整答案,请扫码查看


