《2026年王朝霞考点梳理时习卷九年级数学全一册人教版》

9. 小明、小辉两家所在位置关于学校中心对称.如果小明家距学校$3\ km$，那么他们两家相距6$km$.

答案： 9.6

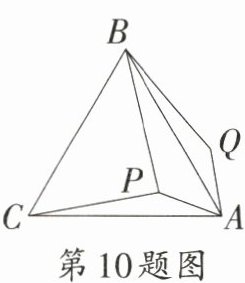
10. [重庆市] 如图，$P$是等边三角形$ABC$内一点，将$\triangle ACP$绕点$A$顺时针旋转$60^{\circ}$得到$\triangle ABQ$，连接$BP$.若$PA = 2$，$PB = 4$，$PC = 2\sqrt{3}$，则四边形$APBQ$的面积为3$\sqrt{3}$.

答案： 10.3$\sqrt{3}$　[解析]连接PQ.由旋转的性质可知，QB = PC = 2$\sqrt{3}$,AQ = PA = 2,∠PAQ = 60°。
∴△APQ为等边三角形。
∴PQ = PA = 2.在△BPQ中,
∵PB² = 16,QB² = 12,PQ² = 4,
∴QB² + PQ² = PB²。
∴△BPQ为直角三角形,∠BQP = 90°。
过点A作AD⊥PQ于点D。
∴PD = $\frac{1}{2}$PQ = 1。
由勾股定理,得AD = $\sqrt{PA² - PD²}$ = $\sqrt{3}$。
∴S四边形APBQ = S△BPQ + S△APQ = $\frac{1}{2}$QB·PQ + $\frac{1}{2}$AD·PQ = 3$\sqrt{3}$。

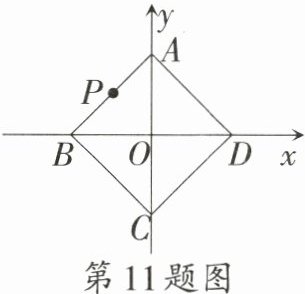
11. 如图，正方形$ABCD$的四个顶点均在坐标轴上，$AB = 2$.将正方形$ABCD$绕点$O$顺时针旋转，每秒旋转$60^{\circ}$，同时点$P$从$AB$的中点处出发，在正方形的边上顺时针移动，每秒移动$1$个单位长度，则第$2028\ s$时，点$P$的坐标为($\frac{\sqrt{2}}{2}$,$-\frac{\sqrt{2}}{2}$).

答案： 11.($\frac{\sqrt{2}}{2}$,$-\frac{\sqrt{2}}{2}$)　[解析]
∵正方形ABCD中,AB = 2,
∴正方形ABCD的周长为8。
∴点P每运动8s为一个循环。
∵$\frac{360}{60°}$ = 6,
∴正方形每旋转6s为一个循环。
∵2028÷6 = 338,2028÷8 = 253……4,
∴第2028s时，正方形回到初始位置，点P从AB的中点处出发，在正方形的边上顺时针移动了4个单位长度，
∴点P位于第四象限，在CD的中点处。
∵CD = AB = 2,OD² + OC² = CD²,OC = OD,
∴OC = OD = $\sqrt{2}$。
∴点C(0,$-\sqrt{2}$),D($\sqrt{2}$,0)。
∴点P($\frac{\sqrt{2}}{2}$,$-\frac{\sqrt{2}}{2}$)

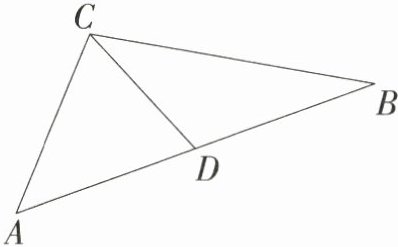
12. ($9$分)如图，在$\triangle ABC$中，点$D$是$AB$边上的中点，已知$AC = 4$，$BC = 6$.
(1)画出$\triangle BCD$关于点$D$的中心对称图形；
(2)根据图形说明线段$CD$长的取值范围.

答案：
12.解:
(1)所作△BCD关于点D的中心对称图形△AED如图所示。　　　　　　　　　　　　(4分)
　　　　　
(2)由
(1)知,△ADE≌△BDC。
∴CD = DE,AE = BC。
∴AE - AC ＜ 2CD ＜ AE + AC,
　　即BC - AC ＜ 2CD ＜ BC + AC。
∴2 ＜ 2CD ＜ 10,即1 ＜ CD ＜ 5。　　　　　　(9分)

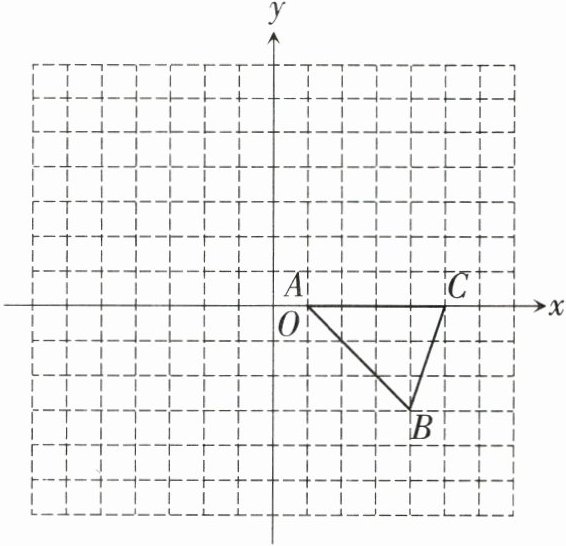
13. [郑州市] ($9$分)如图，在平面直角坐标系中，$\triangle ABC$的顶点为$A(1,0)$，$B(4,-3)$，$C(5,0)$.
(1)平移$\triangle ABC$，若点$C$的对应点$C_1$的坐标为$(7,4)$，画出平移后的$\triangle A_1B_1C_1$；
(2)将$\triangle ABC$以点$(0,0)$为旋转中心旋转$180^{\circ}$，画出旋转后对应的$\triangle A_2B_2C_2$；
(3)已知将$\triangle A_1B_1C_1$绕某一点旋转可以得到$\triangle A_2B_2C_2$，则旋转中心的坐标为(1,2).

答案：
13.解:
(1)△A₁B₁C₁如图所示。　　　　　　　(3分)
(2)△A₂B₂C₂如图所示。　　　　　　　　　(6分)
　　　　 　　　　
(3)(1,2)　　　　　　　　　　　　　　　　(9分)

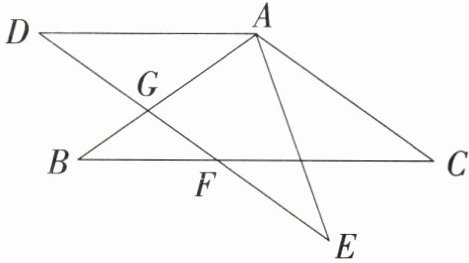
14. ($9$分)如图，在$\triangle ABC$中，$AB = AC$，$\angle BAC = 110^{\circ}$，将$\triangle ABC$绕点$A$顺时针旋转$35^{\circ}$后能与$\triangle ADE$重合，点$G$，$F$分别是$DE$与$AB$，$BC$的交点.
(1)求$\angle AGE$的度数；
(2)求证：四边形$ADFC$是菱形.

答案： 14.解:
(1)
∵AB = AC,∠BAC = 110°,
∴∠B = ∠C = $\frac{1}{2}$(180° - ∠BAC) = 35°。　　　(2分)
　　由旋转的性质知,∠DAB = 35°,∠D = ∠B = 35°。
∴∠AGE = ∠D + ∠DAB = 70°。　　　　　　(4分)
(2)证明:由旋转的性质知,AB = AD。
∵∠DFB = ∠AGE - ∠B = 35°,∠C = 35°,
∴∠D = ∠DFB = ∠C。
∴AC//DF,AD//CF。
∴四边形ADFC是平行四边形。　　　　　(7分)
∵AB = AC,
∴AD = AC。
∴四边形ADFC是菱形。　　　　　　　　　(9分)