《2026年王朝霞考点梳理时习卷九年级数学全一册人教版》

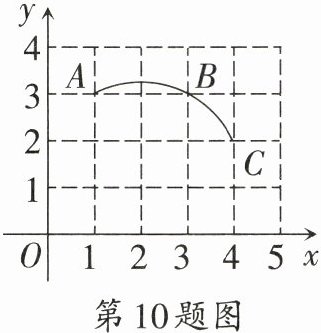
10. 〔北京市〕如图，在平面直角坐标系中，点$A$，$B$，$C$都在格点上，过$A$，$B$，$C$三点作一圆弧，则圆心的坐标是(2,1).

答案： 10.(2,1)

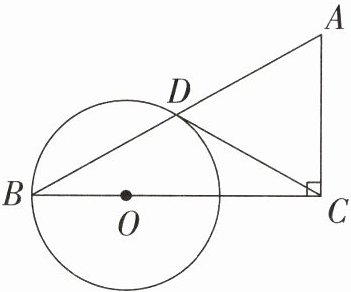
11. 〔重庆市〕如图，$AB$是⊙$O$的直径，点$D$在$BA$的延长线上，$\sqrt{2}OB=OD$，$DC$与⊙$O$相切于点$E$，$BC$与⊙$O$相切于点$B$，交$DE$的延长线于点$C$.若⊙$O$的半径为1，则$EC$的长是$\sqrt{2}$ + 1.

答案： 11.$\sqrt{2}$ + 1　[解析]连接OE.
∵DC切⊙O于点E,
∴∠OED = 90°.
∵⊙O的半径为1,$\sqrt{2}$OB = OD,
∴OD = $\sqrt{2}$.
∴DB = $\sqrt{2}$ + 1.
∵OE = 1,
∴由勾股定理得DE = $\sqrt{OD² - OE²}$ = 1.
∴OE = DE.
∴△OED是等腰直角三角形.
∴∠D = 45°.
∵BC与⊙O相切,
∴∠DBC = 90°.
∴∠C = ∠D = 45°.
∴BC = DB = $\sqrt{2}$ + 1.
∵BC与⊙O相切,DC与⊙O相切,
∴EC = BC = $\sqrt{2}$ + 1.

12. 〔沈阳中考〕(8分)如图，在$\triangle ABC$中，$\angle ACB=90°$，点$O$为$BC$边上一点，以点$O$为圆心，$OB$长为半径的圆与边$AB$相交于点$D$，连接$DC$. 当$DC$为⊙$O$的切线时：
(1)求证：$DC=AC$；
(2)若$DC=DB$，⊙$O$的半径为1，则$DC$的长为$\sqrt{3}$.

答案： 12.解:
(1)证明:连接OD.
∵DC是⊙O的切线,
∴DC ⊥ OD.
∴∠ODC = 90°.
∵∠ACB = 90°,
∴∠BDO + ∠ADC = 90°.
∵∠ACB = 90°,
∴∠A + ∠B = 90°.
∵OB = OD,
∴∠B = ∠BDO.
∴∠A = ∠ADC.
∴DC = AC.
(2)$\sqrt{3}$
[解析]
∵DC = DB,
∴∠DCB = ∠B.
∴∠DCB = ∠B = ∠BDO.
∵∠DCB + ∠B + ∠BDO = 180° - ∠ODC = 90°,
∴∠DCB = 30°.
∵⊙O的半径为1,即OD = 1,
∴OC = 2OD = 2.
∴DC = $\sqrt{OC² - OD²}$ = $\sqrt{3}$.

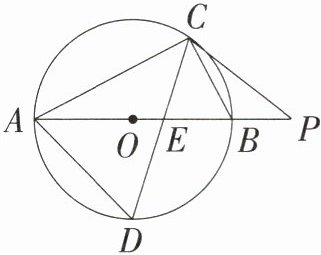
13. (9分)如图，⊙$O$的直径$AB$为5cm，$\angle ACB$的平分线$CD$分别与⊙$O$，$AB$交于点$D$，$E$，$P$为$AB$延长线上一点，且$PC=PE$.
(1)求$AD$的长；
(2)请判断$PC$与⊙$O$的位置关系，并说明理由.

答案：
13.解:
(1)连接BD.
∵AB为⊙O的直径,
∴∠ADB = ∠ACB = 90°.
∵CD平分∠ACB,
∴∠ACD = ∠BCD = 45°.
∴$\overset{\frown}{AD}$ = $\overset{\frown}{BD}$.
∴AD = BD.
∴△ABD为等腰直角三角形.
∵AD² + BD² = AB²,AB = 5cm,
∴2AD² = 25.
∴AD = $\frac{5\sqrt{2}}{2}$cm.
(2)PC与⊙O相切.
理由:如图,连接OC,OD.
　　　　　　　
由
(1)知∠ACD = 45°,
∴∠AOD = 2∠ACD = 90°.
∴∠DOE = 90°.
∴∠ODE + ∠OED = 90°.
∵PC = PE,
∴∠PCE = ∠PEC.
∵∠OED = ∠PEC,
∴∠PCE = ∠OED.
∵OC = OD,
∴∠ODE = ∠OCE.
∴∠PCE + ∠OCE = 90°,即∠OCP = 90°.
∴OC ⊥ CP.
∵OC为⊙O的半径,
∴PC为⊙O的切线,即PC与⊙O相切.

14. (10分)如图，$AB$是⊙$O$的直径，$DO\perp AB$，连接$DA$交⊙$O$于点$C$，过点$C$作⊙$O$的切线交$DO$于点$E$，连接$BC$交$DO$于点$F$.
(1)求证：$CE=EF$.
(2)连接$AF$并延长，交⊙$O$于点$G$. 当$\angle D$的度数为22.5°时，四边形$ECOG$为正方形.

答案： 14.解:
(1)证明:连接OC.
∵CE是⊙O的切线,
∴OC ⊥ CE.
∴∠FCO + ∠ECF = 90°.
∵DO ⊥ AB,
∴∠ABC + ∠BFO = 90°.
∵OC = OB,
∴∠FCO = ∠ABC.
∴∠ECF = ∠BFO.
∵∠CFE = ∠BFO,
∴∠ECF = ∠CFE.
∴CE = EF.
(2)22.5°
[解析]连接OG,EG,OC.当四边形ECOG为正方形时,∠OCE = 90°,∠CEO = ∠COE = 45°.
∵DA交⊙O于点C,
∴OC = OA.
∵DO ⊥ AB于点O,
∴∠DOA = 90°.
∴∠COA = ∠DOA - ∠COE = 45°.
∴∠OAC = 67.5°.
∴∠D = 90° - ∠OAC = 22.5°.