2026年王朝霞考点梳理时习卷九年级数学全一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年王朝霞考点梳理时习卷九年级数学全一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
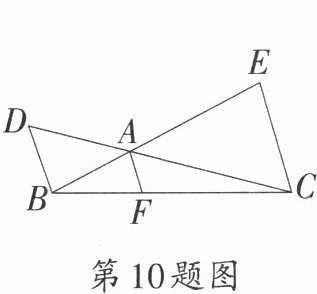
10. 如图,在$\triangle ABC$中,延长$CA$到点$D$,延长$BA$到点$E$,连接$CE,BD,F$是$BC$边上一点,连接$AF$.若$AF // BD // CE$,且$BD = 5 cm$,$CE = 8 cm$,则$S_{\triangle ABD}:S_{\triangle AEC} =$
$\frac{25}{64}$
,$AF =$$\frac{40}{13}$
$cm$.
答案:
10.$\frac{25}{64}$ $\frac{40}{13}$ [解析]
∵BD=5cm,CE=8cm,
∴$\frac{BD}{CE}=\frac{5}{8}$
∵BD//CE,
∴△ABD∽△AEC。
∴$\frac{BD}{CE}=\frac{AB}{AE}=\frac{5}{8}$。
$\frac{S_{\triangle ABD}}{S_{\triangle AEC}}=(\frac{BD}{CE})^{2}=\frac{25}{64}$,$\frac{AB}{BE}=\frac{5}{13}$
∵AF//CE,
∴△ABF∽△EBC。
∴$\frac{AB}{BE}=\frac{AF}{CE}=\frac{5}{13}$,
∵$\frac{AF}{8}=\frac{5}{13}$
∴$AF=\frac{40}{13}$。
∵BD=5cm,CE=8cm,
∴$\frac{BD}{CE}=\frac{5}{8}$
∵BD//CE,
∴△ABD∽△AEC。
∴$\frac{BD}{CE}=\frac{AB}{AE}=\frac{5}{8}$。
$\frac{S_{\triangle ABD}}{S_{\triangle AEC}}=(\frac{BD}{CE})^{2}=\frac{25}{64}$,$\frac{AB}{BE}=\frac{5}{13}$
∵AF//CE,
∴△ABF∽△EBC。
∴$\frac{AB}{BE}=\frac{AF}{CE}=\frac{5}{13}$,
∵$\frac{AF}{8}=\frac{5}{13}$
∴$AF=\frac{40}{13}$。
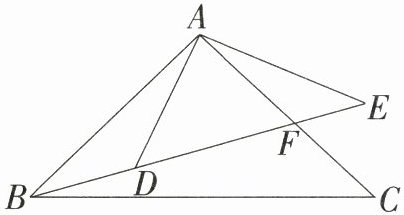
11. (10分)如图,点$B,D,E$在一条直线上,$BE$与$AC$相交于点$F$,$\frac{AB}{AD} = \frac{BC}{DE} = \frac{AC}{AE}$.
(1)求证:$\angle BAD = \angle CAE$;
(2)若$\angle BAD = 21^{\circ}$,求$\angle EBC$的度数.
(1)求证:$\angle BAD = \angle CAE$;
(2)若$\angle BAD = 21^{\circ}$,求$\angle EBC$的度数.

答案:
11.解:
(1)证明:
∵$\frac{AB}{AD}=\frac{BC}{DE}=\frac{AC}{AE}$,
∴△ABC∽△ADE。
∴∠BAC=∠DAE。
∴∠BAC - ∠DAF=∠DAE - ∠DAF,
即∠BAD=∠CAE。
(2)由
(1)知△ABC∽△ADE。
∴∠ABC=∠ADE。
∵∠ABC=∠ABE+∠EBC,∠ADE=∠ABE+∠BAD,
∴∠EBC=∠BAD=21°。
(1)证明:
∵$\frac{AB}{AD}=\frac{BC}{DE}=\frac{AC}{AE}$,
∴△ABC∽△ADE。
∴∠BAC=∠DAE。
∴∠BAC - ∠DAF=∠DAE - ∠DAF,
即∠BAD=∠CAE。
(2)由
(1)知△ABC∽△ADE。
∴∠ABC=∠ADE。
∵∠ABC=∠ABE+∠EBC,∠ADE=∠ABE+∠BAD,
∴∠EBC=∠BAD=21°。
12. 设题新角度 过程性学习(10分)
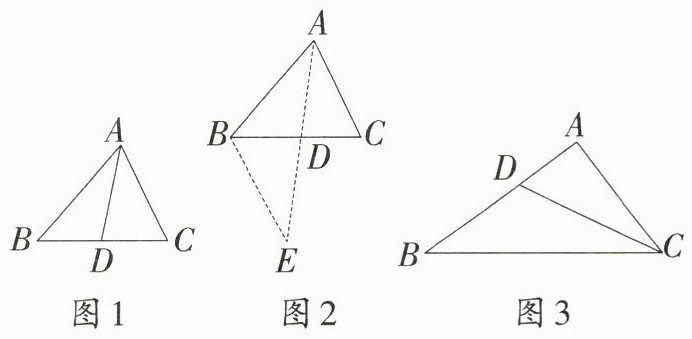
【发现问题】某学习小组发现:三角形一个角的平分线截对边形成的两条线段的比等于这个三角形中对应的两边之比.如图1,在$\triangle ABC$中,$AD$平分$\angle BAC$,则$\frac{BD}{DC} = \frac{AB}{AC}$.
【猜想验证】下面是“发现问题”的不完整的证明过程.
证明:如图2,过点$B$作$BE // AC$,交$AD$的延长线于点$E$……请按照上面的证明思路,补全证明过程;
【拓展应用】如图3,已知$ Rt \triangle ABC$中$\angle BAC = 90^{\circ}$,$AC = 6$,$BC = 10$,$CD$平分$\angle ACB$,则$AD =$
【发现问题】某学习小组发现:三角形一个角的平分线截对边形成的两条线段的比等于这个三角形中对应的两边之比.如图1,在$\triangle ABC$中,$AD$平分$\angle BAC$,则$\frac{BD}{DC} = \frac{AB}{AC}$.
【猜想验证】下面是“发现问题”的不完整的证明过程.
证明:如图2,过点$B$作$BE // AC$,交$AD$的延长线于点$E$……请按照上面的证明思路,补全证明过程;
【拓展应用】如图3,已知$ Rt \triangle ABC$中$\angle BAC = 90^{\circ}$,$AC = 6$,$BC = 10$,$CD$平分$\angle ACB$,则$AD =$
3
.
答案:
12.解:[猜想验证]过点B作BE//AC,交AD的延长线于点E。
∴∠E=∠CAD。
∵∠BDE=∠CDA,
∴△BDE∽△CDA。
∴$\frac{BD}{CD}=\frac{BE}{AC}$
∵AD平分∠BAC,
∴∠BAD=∠CAD。
∴∠BAD=∠E。
∴AB=BE。
$\frac{BD}{CD}=\frac{AB}{AC}$
[拓展应用]3
[解析]
∵∠BAC=90°,AC=6,BC=10,
∴$AB=\sqrt{BC^{2}-AC^{2}}=8$。
∵CD平分∠ACB,
∴与[猜想验证]同理可得$\frac{AD}{BD}=\frac{AC}{BC}$
$\frac{AD}{8 - AD}=\frac{6}{10}$
∴AD=3。
∴∠E=∠CAD。
∵∠BDE=∠CDA,
∴△BDE∽△CDA。
∴$\frac{BD}{CD}=\frac{BE}{AC}$
∵AD平分∠BAC,
∴∠BAD=∠CAD。
∴∠BAD=∠E。
∴AB=BE。
$\frac{BD}{CD}=\frac{AB}{AC}$
[拓展应用]3
[解析]
∵∠BAC=90°,AC=6,BC=10,
∴$AB=\sqrt{BC^{2}-AC^{2}}=8$。
∵CD平分∠ACB,
∴与[猜想验证]同理可得$\frac{AD}{BD}=\frac{AC}{BC}$
$\frac{AD}{8 - AD}=\frac{6}{10}$
∴AD=3。
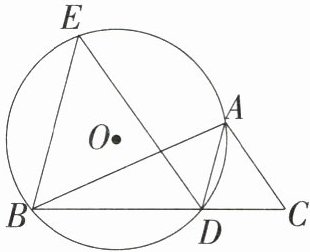
13. (10分)如图,已知$AD$是$\triangle ABC$的角平分线,$\odot O$经过$A,B,D$三点,过点$B$作$BE // AD$,交$\odot O$于点$E$,连接$ED$.
(1)求证:$ED // AC$;
(2)若$BD = 2CD$,设$\triangle EBD$的面积为$S_1$,$\triangle ADC$的面积为$S_2$,且$S_1^2 - 16S_2 + 4 = 0$,求$\triangle ABC$的面积.
(1)求证:$ED // AC$;
(2)若$BD = 2CD$,设$\triangle EBD$的面积为$S_1$,$\triangle ADC$的面积为$S_2$,且$S_1^2 - 16S_2 + 4 = 0$,求$\triangle ABC$的面积.

答案:
13.解:
(1)证明:
∵AD是△ABC的角平分线,
∴∠BAD=∠DAC。
∵∠E=∠BAD,
∴∠E=∠DAC。
∵BE//AD,
∴∠E=∠EDA。
∴∠EDA=∠DAC。
∴ED//AC。
(2)
∵BE//AD,
∴∠EBD=∠ADC。
由
(1)知∠E=∠DAC。
∴△EBD∽△ADC,且相似比为$\frac{BD}{CD}=2$。
∴$\frac{S_{1}}{S_{2}}=4$,即$S_{1}=4S_{2}$。
∵$S^{2}-16S_{2}+4=0$,
∴$16S_{2}^{2}-16S_{2}+4=0$。
∴$S_{2}=\frac{1}{2}$。
$\frac{S_{\triangle ABC}}{S_{2}}=\frac{BC}{CD}=\frac{BD + CD}{CD}=\frac{3CD}{CD}=3$,
∴$S_{\triangle ABC}=3S_{2}=\frac{3}{2}$。
(1)证明:
∵AD是△ABC的角平分线,
∴∠BAD=∠DAC。
∵∠E=∠BAD,
∴∠E=∠DAC。
∵BE//AD,
∴∠E=∠EDA。
∴∠EDA=∠DAC。
∴ED//AC。
(2)
∵BE//AD,
∴∠EBD=∠ADC。
由
(1)知∠E=∠DAC。
∴△EBD∽△ADC,且相似比为$\frac{BD}{CD}=2$。
∴$\frac{S_{1}}{S_{2}}=4$,即$S_{1}=4S_{2}$。
∵$S^{2}-16S_{2}+4=0$,
∴$16S_{2}^{2}-16S_{2}+4=0$。
∴$S_{2}=\frac{1}{2}$。
$\frac{S_{\triangle ABC}}{S_{2}}=\frac{BC}{CD}=\frac{BD + CD}{CD}=\frac{3CD}{CD}=3$,
∴$S_{\triangle ABC}=3S_{2}=\frac{3}{2}$。
查看更多完整答案,请扫码查看


