11. 如图,将一张长方形纸条折一折,若$∠1=35^{\circ }$,则$∠2$等于(

A. $65^{\circ }$
B. $70^{\circ }$
C. $75^{\circ }$
D. $80^{\circ }$
B
).
A. $65^{\circ }$
B. $70^{\circ }$
C. $75^{\circ }$
D. $80^{\circ }$
答案:
B
12. 如图,直线$m// n$,把一块含$45^{\circ }$角的直角三角板ABC按如图所示的方式放置,点B在直线n上,$∠A=90^{\circ }$,若$∠1=25^{\circ }$,则$∠2$等于(

A. $70^{\circ }$
B. $65^{\circ }$
C. $25^{\circ }$
D. $20^{\circ }$
D
).
A. $70^{\circ }$
B. $65^{\circ }$
C. $25^{\circ }$
D. $20^{\circ }$
答案:
D
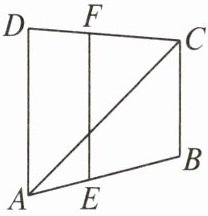
13. 如图,已知$∠DAC=∠ACB,∠D+∠DFE=180^{\circ },EF// BC$吗? 为什么?
解
理由: $ \because \angle DAC = \angle ACB $, $ \therefore $
$ \because \angle D + \angle DFE = 180^{\circ} $, $ \therefore $
$ \because AD // BC $, $ AD // EF $,
$ \therefore $

解
$EF // BC$
.理由: $ \because \angle DAC = \angle ACB $, $ \therefore $
$AD // BC$
.$ \because \angle D + \angle DFE = 180^{\circ} $, $ \therefore $
$AD // EF$
.$ \because AD // BC $, $ AD // EF $,
$ \therefore $
$EF // BC$
.
答案:
解 $EF // BC$.
理由: $ \because \angle DAC = \angle ACB $, $ \therefore AD // BC $.
$ \because \angle D + \angle DFE = 180^{\circ} $, $ \therefore AD // EF $.
$ \because AD // BC $, $ AD // EF $,
$ \therefore EF // BC $.
理由: $ \because \angle DAC = \angle ACB $, $ \therefore AD // BC $.
$ \because \angle D + \angle DFE = 180^{\circ} $, $ \therefore AD // EF $.
$ \because AD // BC $, $ AD // EF $,
$ \therefore EF // BC $.
14. 如图,$MN// CD$,思考解决下列问题:
(1)$∠1+∠2+∠3=$
(2)$∠1+∠2+∠3+∠4=$
(3)试探究$∠1+∠2+∠3+∠4+... +∠m=$
(1)$∠1+∠2+∠3=$
$360^{\circ}$
;(2)$∠1+∠2+∠3+∠4=$
$540^{\circ}$
;(3)试探究$∠1+∠2+∠3+∠4+... +∠m=$
$180^{\circ}(m - 1)$
.
答案:
(1) $360^{\circ}$
(2) $540^{\circ}$
(3) $180^{\circ}(m - 1)$
(1) $360^{\circ}$
(2) $540^{\circ}$
(3) $180^{\circ}(m - 1)$
查看更多完整答案,请扫码查看


