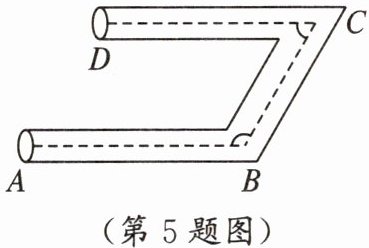
5. 如图,一个弯曲管道$AB// CD,∠ABC=120^{\circ }$,则$∠BCD$的度数为(
A. $120^{\circ }$
B. $30^{\circ }$
C. $60^{\circ }$
D. $150^{\circ }$
C
).
A. $120^{\circ }$
B. $30^{\circ }$
C. $60^{\circ }$
D. $150^{\circ }$
答案:
C
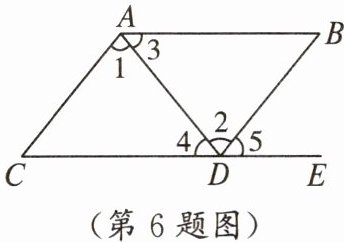
6. 如图,点E在CD的延长线上,下列条件不能判定$AB// CD$的是(
A. $∠1=∠2$
B. $∠3=∠4$
C. $∠5=∠B$
D. $∠B+∠BDC=180^{\circ }$
A
).
A. $∠1=∠2$
B. $∠3=∠4$
C. $∠5=∠B$
D. $∠B+∠BDC=180^{\circ }$
答案:
A
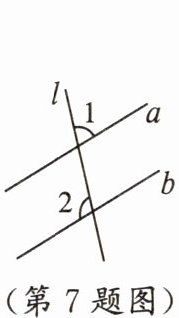
7. 如图,直线l分别与直线a,b相交,$a// b$,若$∠1=71^{\circ }$,则$∠2$的度数为
$109^{\circ}$
.
答案:
$109^{\circ}$
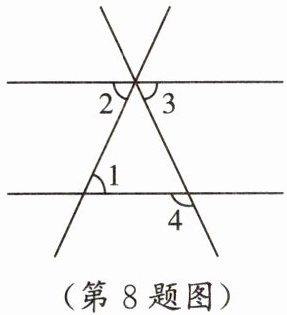
8. 如图,已知$∠1=∠2=∠3=65^{\circ }$,则$∠4=$
$115^{\circ}$
.
答案:
$115^{\circ}$
9. 如图,$∠A=∠CEF,∠1=∠B,DE// BC$吗? 为什么?
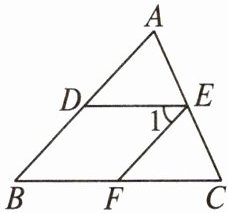
解
理由: $ \because \angle A = \angle CEF $, $ \therefore $
$ \therefore $
$ \because \angle 1 = \angle B $, $ \therefore $
$ \therefore $

解
DE // BC
.理由: $ \because \angle A = \angle CEF $, $ \therefore $
EF // AB
,$ \therefore $
$ \angle EFC = \angle B $
.$ \because \angle 1 = \angle B $, $ \therefore $
$ \angle EFC = \angle 1 $
,$ \therefore $
DE // BC
.
答案:
解 $DE // BC$.
理由: $ \because \angle A = \angle CEF $, $ \therefore EF // AB $,
$ \therefore \angle EFC = \angle B $.
$ \because \angle 1 = \angle B $, $ \therefore \angle EFC = \angle 1 $,
$ \therefore DE // BC $.
理由: $ \because \angle A = \angle CEF $, $ \therefore EF // AB $,
$ \therefore \angle EFC = \angle B $.
$ \because \angle 1 = \angle B $, $ \therefore \angle EFC = \angle 1 $,
$ \therefore DE // BC $.
10. 将一副三角尺(厚度不计)按如图所示摆放,使箭头所指的两条边互相平行,则图中$∠1$的度数为(
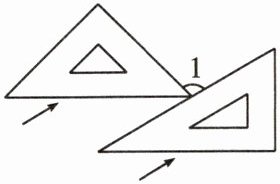
A. $100^{\circ }$
B. $105^{\circ }$
C. $115^{\circ }$
D. $120^{\circ }$
B
).
A. $100^{\circ }$
B. $105^{\circ }$
C. $115^{\circ }$
D. $120^{\circ }$
答案:
B
查看更多完整答案,请扫码查看


