【例题】如图,化简$\sqrt {a^{2}}-|a+b|+\sqrt {(c-a)^{2}}+|b+c|$=

-a+2b+2c
.
答案:
解 由数轴,得$b<a<0<c,|c|>|b|>|a|$,
所以$a+b<0,c-a>0,b+c>0$.
所以原式$=|a|-|a+b|+|c-a|+|b+c|=-a-(-a-b)+(c-a)+(b+c)=-a+a+b+c-a+b+c=-a+2b+2c$.
所以$a+b<0,c-a>0,b+c>0$.
所以原式$=|a|-|a+b|+|c-a|+|b+c|=-a-(-a-b)+(c-a)+(b+c)=-a+a+b+c-a+b+c=-a+2b+2c$.
1. 实数a,b在数轴上的对应点如图所示,化简:$\sqrt {(a-b)^{2}}-\sqrt [3]{(b-1)^{3}}=$
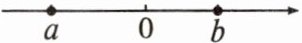
$-a+1$
.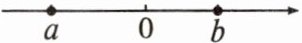
答案:
$-a+1$ 解析 根据数轴上点的位置,得$a<0<b$,所以$a-b<0$,则原式$=|a-b|-(b-1)=b-a-b+1=-a+1.$
2. 实数a,b在数轴上的对应点的位置如图所示,化简:$|a-\sqrt {2}|+|b+\sqrt {2}|-|a-b|$=

2b
.
答案:
解 由数轴,得$a-\sqrt {2}>0,b+\sqrt {2}>0,a-b>0$,故原式$=a-\sqrt {2}+b+\sqrt {2}-(a-b)=a-\sqrt {2}+b+\sqrt {2}-a+b=2b.$
查看更多完整答案,请扫码查看


